SOLUTION: A rectangular field is 200m by 300m. A roadway of width xm is to be built just inside the field. What is the widest the roadway can be and still leave 50,000m^2 in the region?

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: A rectangular field is 200m by 300m. A roadway of width xm is to be built just inside the field. What is the widest the roadway can be and still leave 50,000m^2 in the region?       Log On


   

Question 122670: A rectangular field is 200m by 300m. A roadway of width xm is to be built just inside the field. What is the widest the roadway can be and still leave 50,000m^2 in the region?
60,000 - 400x - 600x +x = 50,000
Am I on the right track for solving the problem with this formula? I feel like I'm missing something.
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
First let's draw a picture. We can see that the length of the inner rectangle is 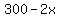300-2x and the width of the inner rectangle is 200-2x since we are taking away 2x from both the length and the width.

note: the inner rectangle represents the remaining area




From the drawing, the area of remaining area is (ie the blue rectangle):

A=%28300-2x%29%28200-2x%29



A=%28300-2x%29%28200-2x%29 Start with the given equation



50000=%28300-2x%29%28200-2x%29 Plug in A=50,000



50000=4x%5E2-1000x%2B60000 Foil



0=4x%5E2-1000x%2B60000-50000 Subtract 50,000 from both sides



0=4x%5E2-1000x%2B10000 Combine like terms


Let's use the quadratic formula to solve for x:


Starting with the general quadratic

ax%5E2%2Bbx%2Bc=0

the general solution using the quadratic equation is:

x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29



So lets solve 4%2Ax%5E2-1000%2Ax%2B10000=0 ( notice a=4, b=-1000, and c=10000)




x+=+%28--1000+%2B-+sqrt%28+%28-1000%29%5E2-4%2A4%2A10000+%29%29%2F%282%2A4%29 Plug in a=4, b=-1000, and c=10000



x+=+%281000+%2B-+sqrt%28+%28-1000%29%5E2-4%2A4%2A10000+%29%29%2F%282%2A4%29 Negate -1000 to get 1000



x+=+%281000+%2B-+sqrt%28+1000000-4%2A4%2A10000+%29%29%2F%282%2A4%29 Square -1000 to get 1000000



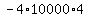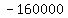
x+=+%281000+%2B-+sqrt%28+1000000%2B-160000+%29%29%2F%282%2A4%29 Multiply -4%2A10000%2A4 to get -160000



x+=+%281000+%2B-+sqrt%28+840000+%29%29%2F%282%2A4%29 Combine like terms in the radicand (everything under the square root)



x+=+%281000+%2B-+200%2Asqrt%2821%29%29%2F%282%2A4%29 Simplify the square root (note: If you need help with simplifying the square root, check out this solver)



x+=+%281000+%2B-+200%2Asqrt%2821%29%29%2F8 Multiply 2 and 4 to get 8

So now the expression breaks down into two parts

x+=+%281000+%2B+200%2Asqrt%2821%29%29%2F8 or x+=+%281000+-+200%2Asqrt%2821%29%29%2F8


Now break up the fraction


x=%2B1000%2F8%2B200%2Asqrt%2821%29%2F8 or x=%2B1000%2F8-200%2Asqrt%2821%29%2F8


Simplify


x=125%2B25%2Asqrt%2821%29 or x=125-25%2Asqrt%2821%29


So these expressions approximate to

x=239.564392373896 or x=10.435607626104


So our possible solutions are:

x=239.564392373896 or x=10.435607626104


However, if you plug in x=239.564392373896 into A=%28300-2x%29%28200-2x%29 , it will give you a negative area, so our only solution is


x=10.435607626104


So the roadway can be about 10.44 m wide which will leave 50,000 m^2 of field