Question 122125: Solve using the quadratic formula
3x squared - 2x + 1 = 0
Answer by bucky(2189)   (Show Source):
You can put this solution on YOUR website! Given the equation:
.
.
To solve this using the quadratic formula, begin by comparing the given equation to the
standard quadratic form of:
.
.
If you compare them term-by-term, you see that "a" which is the multiplier of the x-squared must
be 3. And b which is the multiplier of the x must be -2. And finally, c which is the constant
must be +1. So in solving this equation using the quadratic formula, you use a = +3, b = -2, and
c = +1.
.
The quadratic formula says that any quadratic equation of the form:
.
.
has for its roots the values of x determined by using the equation:
.
.
So all that has to be done to find the values of x is to substitute the appropriate
values of a, b, and c into this equation for x.
.
Using the values of a, b, and c as identified above for this problem, results in the equation
for x becoming:
.
.
The -(-2) becomes just +2. And the denominator of 2*3 becomes 6. These two changes result
in the equation for x being simplified to:
.
.
Next work on simplifying the quantity within the radical sign. Squaring -2 results in
+4 and multiplying -4 times 3 times 1 results in -12. Substituting these results under the
radical simplifies the equation for x to:
.
.
Notice that the term inside the radical sign is negative. This tells you several things. First
it tells you that the graph of the quadratic equation you were given does not cross or touch
the x-axis. And it tells you that the values for x contain an imaginary part.
.
Lets concentrate now on what that imaginary part is by just working on the part of the answer
that involves the radical:
.
.
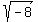
Using the rules of square roots we can simplify this to:
.
.
Next define 
.
Substituting  into the radical (in place of the -1 that multiplies the 2}}} and applying
some rules of radical simplification results in the radical term becoming:
.
.
Going all the way back to the equation for x and substituting this result for the radical
results in:
.
.
Notice that 2 is a common factor of all terms in the numerator and also of the denominator.
Therefore, the factor 2 can be divided into the numerator and denominator and this reduces
the answers to:
.
.
Hope that you can track all the math here so that you can understand where the answer comes
from. And I hope this gives you a little more insight into solving for x in quadratic
equations that have complex roots.
.
|
|
|
