Question 121978: A rectangular flower bed is to be constructed along the front of a house.If there is 30m of landscaping border to be used along the side of the house, determine the dimensions of the flower bed and the maximum area which can be enclosed.
I began with 30=2w+l
30-2w=l and my teacher said this was right so far but I don't know what to do next:(
Found 3 solutions by oscargut, stanbon, bucky:
Answer by oscargut(2103)   (Show Source): (Show Source):
You can put this solution on YOUR website! You have to find the maximum of area = LW as you know L=30-2W
then you have to find maximum of f(W)=(30-2W)W that is maximum when W=7.5 and L=15
Finally maximum area = 15*7.5=112.5
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! A rectangular flower bed is to be constructed along the front of a house.If there is 30m of landscaping border to be used along the side of the house, determine the dimensions of the flower bed and the maximum area which can be enclosed.
I began with 30=2w+l
------------
l=30-2w
Area = l*w = (30-2w)*w
Area = -2w^2+30w
This is a quadratic equation with a=-2 and b=30:
The maximum area occurs when w=-b/2a= -30/(-4) = 7.5 meters
----------------
The dimensions that give maximum area are w=7.5 meters; l = 30-2w= 15 meters.
==================
Cheers,
Stan H.
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'm going to use L for length so we don't confuse it with the number 1. You got:
.
30 - 2W = L
.
and that is correct. Now let's look at the equation for the area of the flowerbed:
.
A = L * W
.
But you found that L = 30 - 2W. So you can substitute 30 - 2W for L in the area equation and
the Area equation then becomes:
.
A = L * W = (30 - 2W)*W
.
When you multiply out the right side the equation simplifies to:
.
Area = 30W - 2W^2
.
Just so we get an idea of what's going on here, let me give you the graph of this. I'm going to
use Area on the y-axis and W on the x-axis to get the graph as:
.
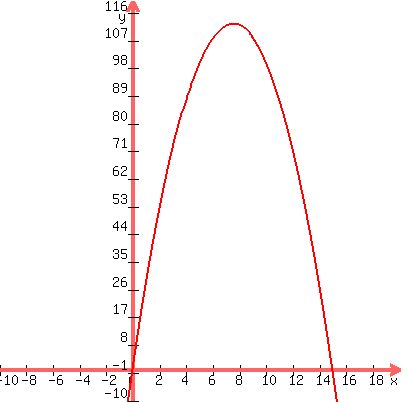
.
Notice on the graph where the peak area occurs. We can find the value of W where the
area will be the maximum (or peak value) in a couple of ways. First, we could return to the
area equation:
.
Area = (30 - 2W) *W
.
The we can set the area equal to zero, just to find where the graph crosses the horizontal
axis. So if we say:
.
0 = (30 - 2W) * W
.
Then we can say that the right side will be zero and equal to the left side if either W = 0
or if (30 - 2W) = 0 ... because either case will result in a multiplication by zero on the
right side ... making the entire right side equal to zero and therefore equal to the left side.
.
So we know the graph crosses the horizontal axis at 0 (when W = 0). And we can find that
.
30 - 2W = 0
.
Subtracting 30 from both sides gives:
.
-2W = -30
.
and dividing both sides by -2 further gives:
.
W = 15
.
So the graph crosses the horizontal axis again at +15.
.
The parabolic graph is symmetrical. That means that the peak of the graph occurs when the
value of W is midway between 0 and 15. So the maximum area occurs when W is 7.5 (this is midway
point and is the average of 0 and 15).
.
Another way to find the value of W where the peak occurs is to use the quadratic formula, if you
are familiar with is. The quadratic formula says that for the standard form of a quadratic equation:
.

.
the values of W that satisfy this equation are:
.

.
Well, when you rearrange your quadratic equation into standard form, it is:
.

.
By comparing this with the standard form you find that a = -2, b = 30, and c = 0.
.
The part of the quadratic equation answer for W that we are interested in is 
.
If you substitute 30 for b and -2 for a in that part you again find that:
.

.
is the value of W that will give you the peak of the area graph.
.
Anyhow, you know that you want the width W to be 7.5 meters. And way back at the top you
found that L = 30 - 2W. So substituting 7.5 for W results in:
.
L = 30 - 2(7.5) = 30 - 15 = 15 meters
.
So, the dimensions of the flowerbed are 7.5 meters by 15 meters and this gives you a
maximum area of 7.5*15 = 112.5 square meters ... which is about what the graph shows.
.
Hope this didn't confuse you too much. Just use the graph as an aid to help you see what is
going on here ... you don't have to graph the equation to get the answer, but I included it
just so you might see what we did rather than just get lost in the math.
.
|
|
|