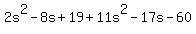What amazes me about such posts as this (and we've had quite a few lately)
is why a teacher of a class already studying completing the square, is bothering
to test students to see whether they understand how to collect like terms.
Collecting like terms is much more elementary than completing the square.
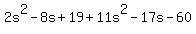Collecting like terms:
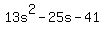Factor 13 out of the first two terms:
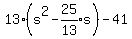To complete the square:
1. Multiply the coefficient of non-squared variable, s, by 1/2
2. Square what you get:
3. Add and then subtract what you got inside the parentheses:
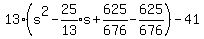Factor the first three terms into two factors exactly alike
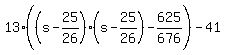Write as the square of a binomial:
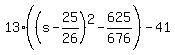We want this to be as small as possible.
This will be smallest when what's in the parentheses is smallest,
and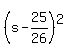 
has smallest value 0, when s=25/26, the
smallest value the expression can take on is
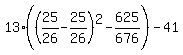
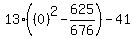
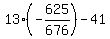Since 13 divides evenly into 676 and gives 52,
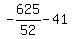Multiply 41 by 52/52 to get a common denominator:
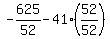
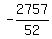<--answer
[And it also amazes me that this teacher would assign problems with
such ugly answers. This teacher should be reprimanded if not fired!]
Edwin
