.
Find the constant p such that x^2 - 5x - 14x + x^2 + p is the square of a binomial.
~~~~~~~~~~~~~~~~~~~~~
Reduce to the standard form quadratic polynomial by combining like terms
2x^2 - 19x + p.
Present it as a square of a binomial
2x^2 - 19x + p = (ax+b)^2.
It is the same as
2x^2 - 19x + p = a^2*x^2 + 2abx + b^2.
Hence,
2 = a^2, or a =  ;
-19 = 2ab, or -19 =
;
-19 = 2ab, or -19 = 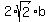 , which gives b =
, which gives b = 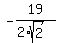 =
= 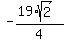 ;
p = b^2 =
;
p = b^2 = 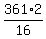 =
=  .
.
Solved.