Question 1209123: Let a and b be the roots of x^2 + 7x - 4 = 0. Find (a + 3)/(b + 3) + (b + 3)/(a + 3).
Found 2 solutions by math_tutor2020, greenestamps:
Answer by math_tutor2020(3816)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: -33/16
--------------------------------------------------------------------------
--------------------------------------------------------------------------
Explanation
I'll use p,q in place of a,b
This is because a,b,c are the standard coefficients of the quadratic template  . .
In the case of x^2+7x-4 = 0 we have a = 1, b = 7, c = -4.
Instead of computing 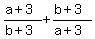 the expression I'll evaluate is the expression I'll evaluate is 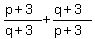
----------------------------------------------
I'll take a slight detour for a moment.
From the quadratic version of Vieta's Formulas, we know that:
p+q = -b/a
p*q = c/a
When plugging a = 1, b = 7, and c = -4, we get
p+q = -b/a = -7/1 = -7
p*q = c/a = -4/1 = -4
In short,
p+q = -7
p*q = -4
Let's call these equation (1) and equation (2) to be used later.
Then note the following


 Applying equations (1) and (2) Applying equations (1) and (2)
 Let's call this equation (3) Let's call this equation (3)
----------------------------------------------
Let's return to 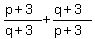
We'll combine the fractions.
Recall we need the LCD to do so.
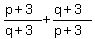
= 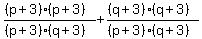
= 
= 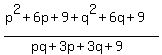
= 
= 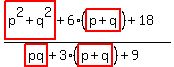
=  Apply equations (1) through (3) Apply equations (1) through (3)
= 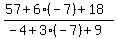
= 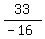
= 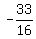
Therefore,

where p,q are the roots of 
----------------------------------------------
To verify, you can use the quadratic formula to solve 
You should get  and and  as the two roots. as the two roots.
Then plug each value into 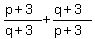 and simplify. and simplify.
I used GeoGebra to verify the answer.
Here's the link to that calculation
https://www.geogebra.org/calculator/fwzwpynj
Let me know if you have any questions.
Answer by greenestamps(13198)   (Show Source): (Show Source):
|
|
|