Question 1206777: What is the range of y = -x^2 - 2x + 3
A. x ≤ 4
B. x ≤ -4
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website! .
What is the range of y = -x^2 - 2x + 3
A. x ≤ 4
B. x ≤ -4
~~~~~~~~~~~~~~~~~~~~~~
Function y(x) is a parabola opened downward.
The vertex is at x = 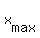 = = "  ' =  = 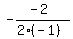-1.
The maximum value of y(x) is at x = -1: 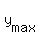 = -(-1)^2 - 2*(-1) + 3 = -1 + 2 + 3 = 4.
In case (A), the value 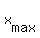= -1 is in the domain; THEREFORE,
the ANSWER to (A) is : at x <=4, the range of y(x) is (-oo,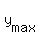] = (-oo,4].
In case (B), the value of 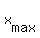= -1 is out the domain of y(x); THEREFORE,
the ANSWER to (B) is : at x <= -4, the range of y(x) is (-oo,y(-4)].
y(-4) = -(-4)^2 - 2*(-4) + 3 = -16 + 8 + 3 = -5; so, the range of y(x) is (-oo,-5].
Solved.
Answer by greenestamps(13198)  (Show Source):
|
|
|
