SOLUTION: In a video game, a bird is flung on a sling shot and follows a parabolic path. The path of the bird can be modeled by the equation h=-16t^2+55t+50 , where h is the height of the

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: In a video game, a bird is flung on a sling shot and follows a parabolic path. The path of the bird can be modeled by the equation h=-16t^2+55t+50 , where h is the height of the      Log On


   

Question 1206162: In a video game, a bird is flung on a sling shot and follows a parabolic path. The path of the bird can be modeled by the equation h=-16t^2+55t+50 , where h
is the height of the bird and t is the amount of time, in seconds, the bird has been in the air. How long will it take the bird to reach a height of 40
feet in the air for the first time? Round your answer to the nearest hundredth.
Answer by ikleyn(52778) About Me  (Show Source):
You can put this solution on YOUR website!
.
In a video game, a bird is flung on a sling shot and follows a parabolic path.
The path of the bird can be modeled by the equation h=-16t^2+55t+50 , where h
is the height of the bird and t is the amount of time, in seconds, the bird has been in the air.
How long will it take the bird to reach a height of 40 feet in the air
for the first time? Round your answer to the nearest hundredth.
~~~~~~~~~~~~~~~~~~~~ 

From the equation, the bird starts at height of 50 feet
and moves up under gravitation at the initial vertical speed of 55 ft/s up; 
then it falls down like a stone, under gravitation.


In short words, solve this quadratic equation

    -16t^2 + 55t + 50 = 40


using the quadratic formula, and take its greatest root.


    +-------------------------------------------------------------+
    |  We take the greatest root, because, as I described above,  |
    |    when the bird is at the height 40 ft first time,         |
    |          it is at this height last time.                    |
    +-------------------------------------------------------------+


The answer is t = 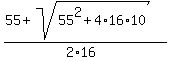%2855+%2B+sqrt%2855%5E2%2B4%2A16%2A10%29%29%2F%282%2A16%29 = 1.96 seconds (rounded).

------------------

In this site,  there is a bunch of lessons on a projectile thrown/shot/launched vertically up

    - Introductory lesson on a projectile thrown-shot-launched vertically up
    - Problem on a projectile moving vertically up and down
    - Problem on an arrow shot vertically upward
    - Problem on a ball thrown vertically up from the top of a tower
    - Problem on a toy rocket launched vertically up from a tall platform
    - A flare is launched from a life raft vertically up

Consider these lessons as your textbook,  handbook,  tutorials and  (free of charge)  home teacher.
Read them attentively and learn on how to solve this type of problems once and for all.