Question 1206103: Find an equation in the form y=ax^2+bx+c for the parabola passing through the points (-1,0),(2,-54),(5,-252)
Found 4 solutions by MathLover1, greenestamps, ikleyn, Edwin McCravy:
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!

given:
( , , ),( ),( , ,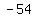 ),( ),( , ,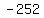 ) )
use ( , , ) )

 .......eq.1 .......eq.1
use ( , ,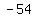 ) )


 .......eq.2 .......eq.2
use ( , ,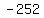 ) )


 .......eq.3 .......eq.3
solve the system:
 .......eq.1 .......eq.1
 .......eq.2 .......eq.2
 .......eq.3 .......eq.3
_________________________
subtract eq.1 from eq.2





 .....eq.1a .....eq.1a
go to
 .......eq.1, substitute .......eq.1, substitute 


 ....eq.2a ....eq.2a
go to
 .......eq.3, substitute .......eq.3, substitute  and and 






go to
 .....eq.1a, substitute .....eq.1a, substitute 



go to
 ....eq.2a, substitute ....eq.2a, substitute 



your equation is:

Answer by greenestamps(13198)   (Show Source): (Show Source):
Answer by ikleyn(52777)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The general approach to solving this and similar problems is to form three equations
for coefficients "a", "b" and "c" of the quadratic function, using the three given points,
then solve this system of three equations.
How you will solve the system, it is just another/separate question.
You may use the solver in your calculator;
or you may use some of numerous online calculators in the Internet;
or do it manually using standard substitution or elimination methods.
Sometimes, some simplifications of this general procedure are possible
if the problem has symmetries that facilitate finding the coefficients.
In this given problem, there are no such symmetries,
so the general approach must be used.
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website! (-1,0),(2,-54),(5,-252)
On your TI-84
Press STAT
Press 1
Using the arrow keys and ENTER,
Enter the 3 given x-coordinates in L1
Enter the 3 given corresponding y-coordinates in L2
Press STAT
Press the right arrow once to highlight CALC
Press 5 for QuadReg
Press the down arrow 4 times to highlight CALCULATE
Press ENTER
You'll see the values for a,b, and c on the screen
y=ax2+bx+c
a=-8
b=-10
c=-2
R2=1
The R2=1 tells us that it's a perfect fit.
Edwin
|
|
|