Question 1205883: The table shows several input and output values of a quadratic
function d(t).
t d(t)
3 3.00
4 5.00
4.5 5.25
5. 5.00
6 3.00
Which statement is true about the function?
Ⓐ The maximum value of d(t) is 6.
Ⓑ The axis of symmetry is t = 5.25.
Ⓒ The range of the function d(t) is 3 < t < 6.
Ⓓ The function d(t) is increasing when t < 4.5.
Found 3 solutions by mccravyedwin, ikleyn, Theo:
Answer by mccravyedwin(406)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Since d(t) is a quadratic function, it is of the form
 . Since we are told that we have 5 solution: . Since we are told that we have 5 solution:
  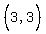
  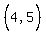
  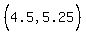
  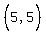
  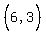 are solutions, we assume they are truthful, pick three
of them, and have the system:
are solutions, we assume they are truthful, pick three
of them, and have the system:

 Solving that system gives A=-1, B=9, C=-15, and we take their word
for it that the other two are solutions, and therefore, the quadratic
equation is:
Solving that system gives A=-1, B=9, C=-15, and we take their word
for it that the other two are solutions, and therefore, the quadratic
equation is:
 We know it is concave downward, because the leading coefficient A=-1 is
negative. So we know it has a maximum value
We use the vertex formula:
We know it is concave downward, because the leading coefficient A=-1 is
negative. So we know it has a maximum value
We use the vertex formula:
  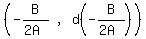  (4.5,5.25), so the maximum value is 5.25
So (A) is false.
The axis of symmetry is
(4.5,5.25), so the maximum value is 5.25
So (A) is false.
The axis of symmetry is    .
So (B) is false.
The range of the function is from negaive infinity to the maximum value, or
the range is .
So (B) is false.
The range of the function is from negaive infinity to the maximum value, or
the range is  So (C) is false.
The function is neither increasing nor decreasing at its maximum
point (4.5,5.25).
So (D) is false.
So they're all false.
Edwin
So (C) is false.
The function is neither increasing nor decreasing at its maximum
point (4.5,5.25).
So (D) is false.
So they're all false.
Edwin
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The answers for (A), (B) and (C) by Edwin are correct.
The answer for (D) by Edwin is incorrect.
The correct answer for (D) is " (D) is TRUE ".
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your solution is selection D.
Ⓓ The function d(t) is increasing when t < 4.5.
the maximum value is at y = 5.25 when x = 4.5
the axis of symmetry is at x = 4.5
the range of the function is 3 <= x <= 6.
it is not 3 < x < 6 because 3 and 6 are the low value and the high value of the range.
you can see that in the following table and graph.
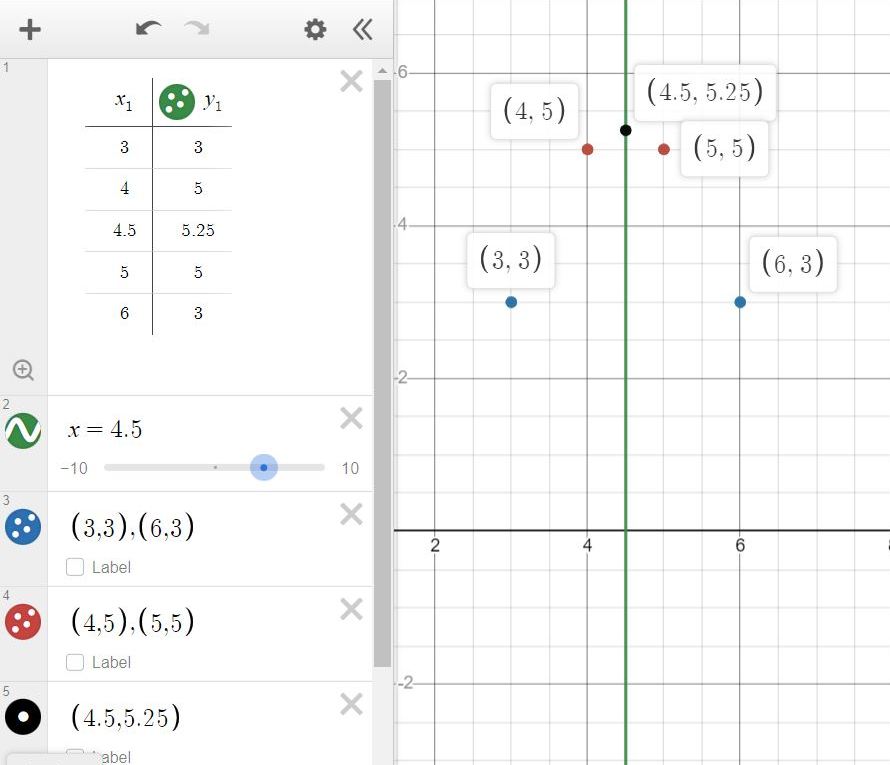
the only selection that is true is selection D.
the functions is increasing when x < 4.5 and decreasing when x > 4.5
the function is maximum when x = 4.5.
|
|
|