Question 1205668: The cables between the two posts onthe Golden Gate Bridge is in the shape of a parabola. The bridge is 535 feet
tall from the road to the top of the support poles and 4100 feet wide. Create an equation in standard and factored form to
represent the shape of the parobola
First write an equation in factored from
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! The standard form of a parabola:

given:
height is  (which is (which is  value of the vertex) value of the vertex)
width is 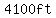
if we place the origin in the midpoint, then we have  from each side of the origin from each side of the origin
than, the vertex is at ( , ,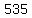 ) and ) and  -intercepts are at ( -intercepts are at (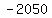 , , ) and ( ) and (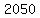 , , ) )
 ....plug in ....plug in  , , 


plug in  , , 

 ....solve for ....solve for 

 ....eq.1 ....eq.1
plug in  , , 

 ....solve for ....solve for 


 ....eq.2 ....eq.2
from eq.1 and eq.2 we have



go to
 ....eq.2, substitute ....eq.2, substitute


your equation is:

The factored form of a parabola:
 , where , where  and and  are the x-intercepts of the parabola are the x-intercepts of the parabola
substitute x-intercepts


Answer by ikleyn(52777)   (Show Source): (Show Source):
|
|
|