Question 1205665: The base of bridge is parabolic in shape. It is 160m wide at the base and 100m high. Determine an algebraic expression, in standard form, that models the shape of the bridge. Draw a diagram and state any assumptions made.
Answer by ikleyn(52778)   (Show Source):
You can put this solution on YOUR website! .
The base of bridge is parabolic in shape. It is 160m wide at the base and 100m high.
Determine an algebraic expression, in standard form, that models the shape of the bridge.
Draw a diagram and state any assumptions made.
~~~~~~~~~~~~~~~~~~~~
This parabola has x-intercepts at x= 0 and x= 160, so we can write
y = a*(x-0)*(x-160), or y = ax*(x-160),
where "a" is a real coefficient, now unknown.
To find it, use the condition that the elevation of the bridge is 100 m at the center
100 = a*80*(80-160), or 100 = -a*6400.
It gives a =  =  .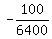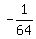
Thus the equation of the parabola is
y =  .
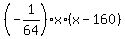Having this equation, you can plot the graph on your own.
Use free of charge plotting tool at web-site www.desmos.com/calculator
Solved.
----------------
Surely, 100 m high is absolutely unrealistic elevation for the bridge.
Probably, 10 m elevation is much more realistic.
|
|
|
