Question 1200523: an open-topped box is constructed from a rectangular piece of cardboard that is twice as long as it is wide by removing a square of size 3 inches from each corner and turning up the edges. If the box is to hold 5,940 in^3, how big should the original piece of cardboard be?
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
an open-topped box is constructed from a rectangular piece of cardboard
that is twice as long as it is wide by removing a square of size 3 inches
from each corner and turning up the edges.
If the box is to hold 5,940 in^3, how big should the original piece of cardboard be?
~~~~~~~~~~~~~~~~~~~
The area of the base of the box is 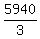 = 1980 in^2.
If x and 2x are the dimensions of the cardboard, then the area equation
for the base is
(x-6)*(2x-6) = 1980 in^2.
Simplify and find x
2x^2 - 12x - 6x + 36 = 1980
2x^2 - 18x - 1944 = 0
x^2 - 9x - 972 = 0
Use the quadratic formula and find the roots to this equation.
They are 36 and -27.
Accept positive root and deny negative one.
ANSWER. The dimensions of the cardboard are 36 inches and 72 inches.
Solved.
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! let L = the length and W equal the width of the rectangular piece of cardboard.
when you cut out 3 inch square from each corner of the cardboard, and fold up 3 inches from the length and the width, you are left with an open box that has the following dimensions.
length = L - 6
width = W - 6
height = 3
the volume of the open top box is equal to length * width * height which is equal to (L - 6) * (W - 6) * 3
since the length of the box is twice as long as it is wide, then you get L = 2W and the dimensions of the open top box are (2W - 6) * (W - 6) * 3
simplify this to get 2W * (W - 6) - 6 * (W - 6) * 3
simplify further to get (2W^2 - 12W - 6W + 36) * 3
simplify further to get 6W^2 - 36W - 18W + 108
combine like terms to get 6W^2 - 54W + 108
that's the volume of the open top box.
since the volume is 5940 cubic inches, you get:
6W^2 - 54W + 108 = 5940
subtract 5940 from both sides of the equation to get:
6W^2 - 54W - 5832 = 0
divide both sides of this equation by 6 to get:
W^2 - 54W - 972 = 0
factor this quadratic eqution to get:
W = -27 or plus 36.
W can't be negative, you are left with W = 36
since length is twice the width, you have:
W = 36
L = 72
the dimensions of the open top box are:
length = L - 6 = 66
width = W - 6 = 30
height = 3
the volume of the open top box is therefore 66 * 30 * 3 = 5940 cubic inches.
the original piece of cardboard should have a length of 36 and a width of 72.
|
|
|
