Question 1199655: a ball is thrown from a building that is 50 m tall. the ball reaches an optimal value of 75m after 2 seconds and reaches the ground after 6 seconds. determine the equation of the ball's path in vertex form
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
a ball is thrown from a building that is 50 m tall.
the ball reaches an  maximum maximum  height height
of 75m after 2 seconds and reaches the ground after 6 seconds.
determine the equation of the ball's path in vertex form
~~~~~~~~~~~~~~~~~~~
Based on the given information, we can write the governing equation in this form
h(t) = 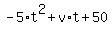 .
In this equation, coefficient 5 at .
In this equation, coefficient 5 at  is half of the gravity acceleration,
which is 10 m/s^2 (or, more precisely, we take this value of 10 m/s^2 for the gravity
acceleration as an approximation, instead of its true value of 9.81 m/s^2).
Next, the constant term of 50 in this equation represents the initial height of 50 m.
Coefficient "v" is the only value, which we do not know now.
This value is the starting velocity.
There is one more agreement, which is commonly accepted in this class
of problems: the coordinate axis for the height is directed vertically up.
It dictates the signs of the terms with is half of the gravity acceleration,
which is 10 m/s^2 (or, more precisely, we take this value of 10 m/s^2 for the gravity
acceleration as an approximation, instead of its true value of 9.81 m/s^2).
Next, the constant term of 50 in this equation represents the initial height of 50 m.
Coefficient "v" is the only value, which we do not know now.
This value is the starting velocity.
There is one more agreement, which is commonly accepted in this class
of problems: the coordinate axis for the height is directed vertically up.
It dictates the signs of the terms with  and with "t".
To find the starting velocity, we can use the given condition about reaching the maximum height.
The theory says that the maximum height is achieved at t = and with "t".
To find the starting velocity, we can use the given condition about reaching the maximum height.
The theory says that the maximum height is achieved at t =  , referring to coefficients
of the general form equation.
In your case a = -5, , referring to coefficients
of the general form equation.
In your case a = -5, 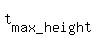 = 2, and it gives you this equation for v = 2, and it gives you this equation for v
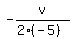 = 2,
or = 2,
or
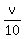 = 2,
v = 2*10 = 20.
Thus, the initial vertical velocity is 20 m/s, and your governing equation for the height is
h(t) = = 2,
v = 2*10 = 20.
Thus, the initial vertical velocity is 20 m/s, and your governing equation for the height is
h(t) = 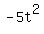 + 20t + 50. ANSWER + 20t + 50. ANSWER
Solved, with full and complete explanations.
-----------------
The rest of the information given in the problem is EXCESSIVE:
it is not necessary for the solution, and we DO NOT USE it.
Moreover, the given value 75 m for the maximum height is INCORRECT
and is NOT CONSISTENT with the given time of 2 seconds :
it is only PURE FANTASY of a problem's composer.
The correct value for the maximum height is 70 m in this problem,
and it CAN NOT be different - otherwise it is not consistent
with the Physics laws.
The time "6 seconds" in the problem is incorrect and inconsistent with
2 seconds given to reach the maximum height.
My DIAGNOSIS after writing my solution is that the problem,
as it is presented in the post,
is composed by a person UNFAMILIAR with the subject.
AS I SEE IT SEVERAL TIMES per day EACH and EVERY DAY at this forum.
I tried to teach you the truth as much as I could.
//////////////////
For more info, look into the lessons
- Introductory lesson on a projectile thrown-shot-launched vertically up
- Problem on a projectile moving vertically up and down
- Problem on an arrow shot vertically upward
- Problem on a ball thrown vertically up from the top of a tower
- Problem on a toy rocket launched vertically up from a tall platform
in this site.
Consider these lessons as your textbook, handbook, tutorials and (free of charge) home teacher.
Read them attentively and learn how to solve this type of problems once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic "Projectiles launched/thrown and moving vertically up and dawn".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|