Question 1199157: Show that the real solutions of the equation ax^2 + bx + c = 0 are the reciprocation the real solutions of the equation cx^2 + bx + a = 0. Assume that b^2 - 4ac is greater than or equal to 0.
Can someone get me started here?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Show that the real solutions of the equation ax^2 + bx + c = 0 are the reciprocation
the real solutions of the equation cx^2 + bx + a = 0.
Assume that b^2 - 4ac is greater than or equal to 0.
Can someone get me started here?
~~~~~~~~~~~~~~~~~
As given, the problem's formulation is not 100% accurate.
To be accurate, it must assume that the coefficient "c" is not zero,
because otherwise an equation cx^2 + bx + a = 0 IS NOT a QUADRATIC.
This assumption is equivalent to say that no one of the routes of
the original equation is 0 (zero).
It is a NECESSARY condition to that the reciprocal to the roots do exist.
So, in my solution below I will assume that a=/=0, c=/=0.
Let x be a root of the equation ax^2 + bx + c = 0.
Since c=/= 0, it implies that x=/=0, so the reciprocal  does exist.
Divide equation does exist.
Divide equation  = 0 by = 0 by  . You will get . You will get
 = 0.
It means that = 0.
It means that  is the root of the equation is the root of the equation 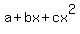 = 0. = 0.
Q.E.D.
Solved.
////////////////
By the way, the statement of the problem is true for complex roots, too,
as it is true for real roots.
The same formal proof works for the complex root.
So, the requirement of the problem to the roots to be real is not necessary: it is EXCESSIVE.
|
|
|