Question 1199009: A ball is thrown upward from 3 meters above ground level with a velocity of 14 meters per second. When does the ball hit the ground?
Here's the explanation:
1. The height starts at 3 meters.
2. It travels at 14 meters pee second or 14(m/s).
In solution step 2 we are told that 14(m/s) = 14t, where t is in seconds.
Where did t come from?
3. Gravity pulls the ball down changing its position by about 5 meters per second squared.
Where did 5 meters per second squared come from?
We are told that it is written like this -5t^2.
Where did the minus 5 come from?
We are further told that -5t^2 is simplified from -(1/2)at^2, where a = 9.8 m/(s^2).
Where did this value of a come from?
The equation created by the given information is h = 3 + 14t - 5t^2.
In my opinion, none of this is given in the given application.
You say?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The STANDARD formula for the height of a projectile launched vertically up is
h(t) = -at^2 + bt + c, (1)
where "a", "b" and "c" are real numbers, a > 0. In this formula
(a) the initial height is equal to the coefficient "c" value;
(b) the initial velocity is the coefficient "b" in the formula;
(c) the coefficient "a" value is half of the gravity acceleration.
For the Earth conditions, the gravity acceleration is g = 9.81 m/s^2, or 32 ft/s^2.
THEREFORE, if you use meters for height, you may use the approximate value of g = 10 m/s^2.
So, in this case a =  = 5 (the numerical value).
ALTERNATIVELY, if you use feet for height, you should use the approximate value of g = 32 ft/s^2.
So, in this case a = = 5 (the numerical value).
ALTERNATIVELY, if you use feet for height, you should use the approximate value of g = 32 ft/s^2.
So, in this case a =  = 16 (the numerical value).
(d) To find the height at the time moment "t", simply substitute the value of "t" into the formula (1) and calculate.
(e) To find the time "t" when the height has a given value h = = 16 (the numerical value).
(d) To find the height at the time moment "t", simply substitute the value of "t" into the formula (1) and calculate.
(e) To find the time "t" when the height has a given value h =  , substitute h = , substitute h =  into equation (1)
and solve equation
h(t) = -at^2 + bt + c = into equation (1)
and solve equation
h(t) = -at^2 + bt + c =  . (2)
(f) To find the time when the height is maximal, use the formula . (2)
(f) To find the time when the height is maximal, use the formula
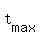 = = 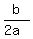 . (3)
(g) To find the maximal height, substitute the time value t= . (3)
(g) To find the maximal height, substitute the time value t= 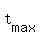 of the formula (3) into the formula (1). of the formula (3) into the formula (1).
That's all you need to know.
---------------
To see numerous examples of solved problems, look into the lessons
- Problem on a projectile moving vertically up and down
- Problem on an arrow shot vertically upward
- Problem on a ball thrown vertically up from the top of a tower
- Problem on a toy rocket launched vertically up from a tall platform
in this site.
Consider these lessons as your textbook, handbook, tutorials and (free of charge) home teacher.
Read them attentively and learn how to solve this type of problems once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic "Projectiles launched/thrown and moving vertically up and dawn".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
////////////////
Comment from student : To find out when the ball will hit the ground,
let h = 0 and solve for t. h = 3 + 14t - 5t^2. 0 = 3 + 14t - 5t^2. Yes?
My response : Yes. Correct.
|
|
|