Question 1198745: Find the quadratic function y = a (x-h)^2 whose graph passes through the given points. (12, -1) and (9, 0)
Found 3 solutions by ikleyn, greenestamps, math_tutor2020:
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the quadratic function y = a (x-h)^2 whose graph passes through the given points.
(12, -1) and (9, 0)
~~~~~~~~~~~~~~~~~~~~~~~
First use the info, which goes with the point (9,0).
It gives you this equation 0 = a*(9-h)^2,
from which you conclude that h = 9.
Now use the info, which goes with the point (12,-1).
It gives you this equation -1 = a*(12-9)^2, or -1 = a*9, a = 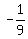 .
Thus the quadratic function is y = .
Thus the quadratic function is y = 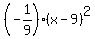 . ANSWER . ANSWER
Solved step by step, with explanations.
////////////////
The reasons by @greenestamps are incorrect.
The given form parabola is not a general form parabola, where three points are needed to define it by an unique way.
It is VERY SPECIAL form of parabolas that touch x-axis.
For this special form, two given points are just ENOUGH to determine the parabola by an unique way,
as I did it in my solution.
Of the three parabolas in the plot by @greenestamps, only one touches x-axis.
It is the parabola shown in red, and only this parabola has the assigned form.
My solution is correct.
@greenestamps reasons and solution is not correct.
The problem is not deficient, as @greenestamps states.
It is posed correctly and has a unique solution, which I found in my post.
For your better understanding, the general form parabola has three parameters,
and, therefore, requires three points to be determined by a unique way.
Parabola, assigned in the post, just has a vertex on x-axis and, therefore,
depends on two parameters, "a" and "h", ONLY.
It is why having two points is ENOUGH to determine this parabola by a unique way.
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
****************************************************
Ignore the solution below.
Tutor @ikleyn's comments are correct. There are an infinite number of quadratic functions that pass through the two given points; however, the given form of the quadratic function "y = a(x-h)^2" is of a function whose graph has its vertex on the x-axis.
There is only one such quadratic function -- the one she shows in her response.
***************************************************
Actually, there is some good mathematics in my solution.... But it doesn't answer the question that is asked.
***************************************************
The problem is deficient; there are an infinite number of quadratic functions whose graphs pass through the two given points.
Two points determine a unique straight line (linear function).
Three points are needed to determine a unique parabola (quadratic function).
Two points determine only an infinite family of quadratic functions.
Use the standard form of a quadratic equation

with the given two points to find parametric equations for the coefficients a, b, and c.
(12,-1): 144a+12b+c = -1
(9,0): 81a+9b+c = 0
Subtract one equation from the other to eliminate c:
63a+3b = -1
Solve for b in terms of a:
b = (-63a-1)/3
Substitute that expression for b in either original equation to find c in terms of a:
81a+9((-63a-1)/3)+c = 0
81a-189a-3 + c = 0
c = 108a+3
Use t as a parameter to get parametric equations for a, b, and c.
a = t
b = (-63t-1)/3
c = 108t+3
t = (-1/9) gives the quadratic function shown by the other tutor (which has the given point (9,0) as the vertex):
a = t = -1/9
b = (-63(-1/9)-1)/3 = (7-1)/3 = 2
c = 108(-1/9)+3 = -12+3 = -9
y = (-1/9)x^2+2x-9
Choose a couple of other values for parameter t to find other quadratic functions that pass through the two given points.
t = 1
a = 1
b = (-63-1)/3 = -64/3
c = 108+3 = 111
y = x^2-(64/3)x+111
t = -1
a = -1
b = (63-1)/3 = 62/3
c = -108+4 = -105
y = -x^2+(62/3)x-105
Here are graphs of those three quadratic functions graphed in the same window x from 0 to 20 and y from-10 to 10, showing all three parabolas passing through the two given points (9,0) and (12,-1):

Answer by math_tutor2020(3816)   (Show Source): (Show Source):
|
|
|