Question 1194459: Find a quadratic model in standard form for (0,0), (1,-5), (2,0)
Answer by ikleyn(52785)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find a quadratic model in standard form for (0,0), (1,-5), (2,0)
~~~~~~~~~~~~~~~~~~
You are looking to find a quiadratic finction in the form
y = ax^2 + bx + c (1)
such that its plot goes through three given points.
Notice that two given points, (0,0) and (2,0), have the same (identical) y-values.
Moreover, these y-values are zeros, so these points are two y-intercepts of the parabola.
Hence, the parabola's symmetry axis is half-way between x-coordinates of these points:
 = = 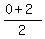 = 1.
So, the parabola in the vertex form is
y = = 1.
So, the parabola in the vertex form is
y = 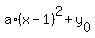 , (2)
where , (2)
where  is the vertex' y-coordinate.
From the other side, you see that the second given point has x-coordinate equal to 1 - hence,
this point is the vertex; so you conclude that in formula (2) is the vertex' y-coordinate.
From the other side, you see that the second given point has x-coordinate equal to 1 - hence,
this point is the vertex; so you conclude that in formula (2)  = -5.
Thus you can write the parabola's expression in the vertex form
y = = -5.
Thus you can write the parabola's expression in the vertex form
y = 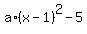 . (3)
Now, to determine the unknown coefficient "a", substitute x= 0 into formula (3) and use
the given info y(0) = 0 (the coordinates of the first point)
0 = . (3)
Now, to determine the unknown coefficient "a", substitute x= 0 into formula (3) and use
the given info y(0) = 0 (the coordinates of the first point)
0 = 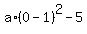 ,
or
0 = a - 5,
which gives you
a = 5.
Now the parabola in vertex form is y = ,
or
0 = a - 5,
which gives you
a = 5.
Now the parabola in vertex form is y = 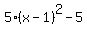 .
To get the standard form, make FOIL
y(x) = 5x^2 - 10x.
It is your ANSWER. .
To get the standard form, make FOIL
y(x) = 5x^2 - 10x.
It is your ANSWER.
Solved.
It is one of possible ways to analyse.
There is another way: it is to write the quadratic form in the form
y = 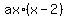 , ,
based on the fact that x= 0 and x= 2 are the zeroes, and then to find the coefficient " a ",
using info about the point (1,-5).
|
|
|