SOLUTION: Doris walks 89 feet diagonally across a rectangular field. She then returns to her starting position along the outside of the field. The total distance she walks is 208 feet. What

Let x and y be the dimensions of the rectangle.

Then from the given part of the problem, we have these two independent equations

     =                (1)    (the diagonal)

     + x + y = 208      (2)    (the total distance)


In the second equation, replace   by 89, based on equation (1).
Keep first equation as is.  Then you get this simplified system

     =        (1')    

    89 + x + y = 208      (2') 


You can simplify it further  

     =        (1'')    

    x + y = 119           (2'')             (because  208-89 = 119).


Next step square equation (2'');  keep equation (1'') as is

     =              (3)

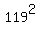     =        (4)


Now subtract equation (3) from equation (4).  You will get

    2xy = 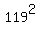 -  = 6240

or

    xy = 3120.         (5)


Now combine equations (2'') and (5) into one system

    x + y = 119        (6)

    xy    = 3120.      (7)


It admits straightforward solution.  From equation (6), express x = 119-y
and substitute it into equation (7).  You will get a quadratic equation

    (119-y)*y = 3120,

or

    y^2 - 119y + 3120 = 0.


You can solve it by factoring or by applying the quadratic formula.


In any case, the factoring is

    (x-80)*(x-39) = 0


and the roots are  80 and 39.


These roots give the dimensions of the rectangle.


ANSWER.  The dimensions of the rectangle are 80 feet by 39 feet.