Question 1193026: What is the maximum product of 2 numbers whose sum is 45? What numbers yield this product?
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
What is the maximum product of 2 numbers whose sum is 45? What numbers yield this product?
~~~~~~~~~~~~~~~~
Let x and y be the numbers; let x be the lesser number and y be the greater number.
Consider the mean value a = 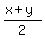 = = 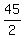 = 22.5 and half the distance between x and y, b = = 22.5 and half the distance between x and y, b = 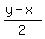 Then, obviously, x = 22.5 - b and y = 22.5 + b, so we can write
xy = (22.5-b)*(22.5+b) =
Then, obviously, x = 22.5 - b and y = 22.5 + b, so we can write
xy = (22.5-b)*(22.5+b) = 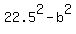 .
From this formula, it is clear that xy is maximum when b= 0, i.e. when the numbers x and y are equal: x = y.
Thus we get that the maximum of the product xy is achieved when x = y.
Together with x + y = 45 it implies that the maximum is achieved in this problem at x = y = 45/2 = 22.5.
The maximum value of xy is then .
From this formula, it is clear that xy is maximum when b= 0, i.e. when the numbers x and y are equal: x = y.
Thus we get that the maximum of the product xy is achieved when x = y.
Together with x + y = 45 it implies that the maximum is achieved in this problem at x = y = 45/2 = 22.5.
The maximum value of xy is then 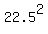 = 506.25.
ANSWER. The maximum is achieved when both numbers are equal to half of the sum, i.e. 22.5.
The maximum value of the product is 506.25 then. = 506.25.
ANSWER. The maximum is achieved when both numbers are equal to half of the sum, i.e. 22.5.
The maximum value of the product is 506.25 then.
Solved.
----------------
There are many different ways and methods of solving such problems.
They differ in the level of necessary prerequisites, which the reader should know to understand the solution.
What I exposed here, is traditionally considered in Math and in Math popular literature as
the SIMPLEST method of solving, accessible for students with minimal level of knowledge (for the most young readers).
|
|
|