Question 1189964: 1. If r varies directly as s and inversely as the square of u, and r = 2 when s = 18 and u= 2, find:
a. r when u = 3 and s =27.
b. s when u = 2 and r = 4.
c. u when r = 1 and s = 36.
please show your solution.
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1. If r varies directly as s and inversely as the square of u, and r = 2 when s = 18 and u= 2, find:
a. r when u = 3 and s =27.
b. s when u = 2 and r = 4.
c. u when r = 1 and s = 36.
please show your solution.
~~~~~~~~~~~~~~
If r varies directly as s and inversely as the square of u, it means that
r =  , (1)
where the coefficient "k" is a constant, now unknown.
To find "k", use the given condition that r= 2 wnen s= 18 and u= 2.
Substitute these values into equation (1). It will give you
2 = , (1)
where the coefficient "k" is a constant, now unknown.
To find "k", use the given condition that r= 2 wnen s= 18 and u= 2.
Substitute these values into equation (1). It will give you
2 = 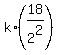 ,
or
2 = ,
or
2 = 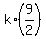 .
Hence, k = .
Hence, k =  = =  .
So, the formula (1) takes the form
r = .
So, the formula (1) takes the form
r = 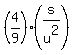 .
Now you know "r" as a function of "s" and "u" and can calculate "r" for any given values of "s" and "u".
For example, in case (a) r = .
Now you know "r" as a function of "s" and "u" and can calculate "r" for any given values of "s" and "u".
For example, in case (a) r = 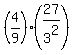 = = 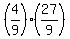 = = 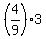 = = 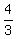 .
Similarly, you can calculate values of "r" in cases (b) and (c).
Make this calculations on your own to make sure that you do understand the procedure.
You may report me about your progress. .
Similarly, you can calculate values of "r" in cases (b) and (c).
Make this calculations on your own to make sure that you do understand the procedure.
You may report me about your progress.
Solved.
|
|
|