SOLUTION: A quadratic equation is given by y=2x^2 - 6bx+3.What is the value of 'b' if the equation of the axis of symmetry is x=9 ? I think the answer is 6 but I really don't fully understan

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: A quadratic equation is given by y=2x^2 - 6bx+3.What is the value of 'b' if the equation of the axis of symmetry is x=9 ? I think the answer is 6 but I really don't fully understan      Log On


   

Question 118946: A quadratic equation is given by y=2x^2 - 6bx+3.What is the value of 'b' if the equation of the axis of symmetry is x=9 ? I think the answer is 6 but I really don't fully understand, can someone please explain this to me ?
Found 5 solutions by jim_thompson5910, stanbon, Earlsdon, josmiceli, scott8148:
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
To find the axis of symmetry, take the x coefficient -6b and divide it by 2%2A2 and negate it. Remember, for y=2x%5E2+-+6bx%2B3, the axis of symmetry is x=-b%2F2a. So in our case, x=-%28-6b%29%2F%282%2A2%29. Since the axis of symmetry is x=9, this means


9=-%28-6b%29%2F%282%2A2%29 Plug in x=9


9=6b%2F%282%2A2%29 Negate -6b


9=6b%2F4 Multiply



36=6b Multiply both sides by 4


6=b Divide both sides by 6


So our answer is b=6. So you are correct.

If we plug in b=6 into y=2x%5E2+-+6bx%2B3, we get

y=2x%5E2+-+6%286%29x%2B3 Plug in b=6



y=2x%5E2+-+36x%2B3 Multiply


Now let's graph


+graph%28+500%2C+500%2C+-30%2C+30%2C+-160%2C+10%2C+2x%5E2+-+36x%2B3%29+


So we can see that the axis of symmetry is x=9. So this verifies our answer.

Answer by stanbon(75887) About Me  (Show Source):
You can put this solution on YOUR website!
A quadratic equation is given by y=2x^2 - 6bx+3.What is the value of 'b' if the equation of the axis of symmetry is x=9 ? I think the answer is 6 but I really don't fully understand, can someone please explain this to me ?
-------------
In the general form of a quadratic. y = ax^2+bx+c,
the axis of symmetry is x = -b/2a Where "b" is the coefficient of the 2nd term.
In Your Problem, "b" = -6b
So -(-6b)/(2*2) = 9
3b/2 = 9
b = 6
-----------
Cheers,
Stan H.

Answer by Earlsdon(6294) About Me  (Show Source):
You can put this solution on YOUR website!
Given y+=+2x%5E2-6bx%2B3, find the value of b if the axis of symmetry is x = 9.
The axis of symmetry of a quadratic equation is given by: x+=+-b%2F2a.
The a and the b come from the general form of the equation: y+=+ax%5E2%2Bbx%2Bc
Since you are given the axis of symmetry as x+=+9, you can write:
x+=+-b%2F2a Substituting a = 2 and b = -6b, and x = 9, you get:
9+=+-%28-6b%29%2F2%282%29 Simplifying this:
9+=+6b%2F4 Multiply both sides by 4.
36+=+6b Finally, divide both sides by 6.
6+=+b...which matches your answer.

Answer by josmiceli(19441) About Me  (Show Source):
You can put this solution on YOUR website!
I always refer beck to the quadratic formula when
I have an axis of symmetry problem.The formula is:
x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+
This finds the x-intercepts (roots)
when the equation is in the form y+=+ax%5E2+%2B+bx+%2B+c
You can rewrite this formula as:
x+=+-b%2F%282%2Aa%29+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%2F%282%2Aa%29+
Think about what this says. It says " The axis of symmetry
is at -b%2F%282%2Aa%29 and the roots are equally spaced on
either side, one on the minus side and one on the plus side
In the given equation, 2x%5E2+-+6Bx+%2B+3, -6B
represents b in the quadratic formula (I used "B" to avoid
confusion). a+=+2 is the other variable.
-b%2F%282%2Aa%29+=+-%28-6B%29%2F%282%2A2%29
-b%2F%282%2Aa%29+=+6B%2F4
The problem tells me this axis of symmetry is at x=9, so
6B%2F4+=+9
solve for B
6B+=+36
B+=+6 answer
The equation turns out to be y+=+2x%5E2+-36x+%2B+3
I'll plot this
+graph%28+600%2C+600%2C+-5%2C+20%2C+-200%2C+30%2C+2x%5E2+-+36x+%2B+3%29+
This shows the answer is OK

Answer by scott8148(6628) About Me  (Show Source):
You can put this solution on YOUR website!
for a quadratic of the form ax^2+bx+c, the equation for the axis of symmetry is x=-b/2a

in this case 9=-(-6b)/(2*2) __ 36=6b __ 6=b

looking at the quadratic formula can help to clarify
___ the formula gives two solutions 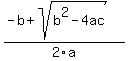%28-b%2Bsqrt%28b%5E2-4ac%29%29%2F2a and %28-b-sqrt%28b%5E2-4ac%29%29%2F2a

the average of the two solutions (which is the midline of the graph) is -b/2a
__ the square root portions cancel each other