SOLUTION: Determine the restrictions on the y-intercept so that y = 3x^2 + 6x - 1 intersects with a line with slope 2 in more than one place.

            Determine the restrictions on the y-intercept of the straight line of the slope 2

            so it intersect the curve y = 3x^2 + 6x - 1 in more than one point.

The straight line equation is  y = 2x + k,  where "k" is the y-interception value.

We should determine this value of "k" from the condition that the equation

    3x^2 + 6x - 1 = 2x + k


has more than one solution.


We rewrite this equation in standard quadratic form

    3x^2 + 4x - (k+1) = 0.


The condition that it has more than one real solution means that the discriminant is positive

    d = b^2 - 4ac > 0,  where  a= 3;  b= 4  and  c= -(k+1).


So, the discriminant is  

    d = 16 + 4*3*(k+1) = 16 + 12(k+1).


The condition d > o is

    16 + 12(k+1) > 0

or

    12(k+1) > -16

       k+1 > -  = -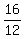 

         k > -  - 1 = - .


ANSWER.  The y-intercept "k" must be greater than  -  = -2  :  k > -2 .