SOLUTION: What is the co-efficient of {{{ x^10 }}} in the following expressions: (A) 1 + (1 + x) + (1 + x)^2 + ... + (1 + x)^20 (B) (1 + x)^2 + (1 + x)^3 + (1 + x)^4 + (1 + x)^5 + .... + (

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: What is the co-efficient of {{{ x^10 }}} in the following expressions: (A) 1 + (1 + x) + (1 + x)^2 + ... + (1 + x)^20 (B) (1 + x)^2 + (1 + x)^3 + (1 + x)^4 + (1 + x)^5 + .... + (      Log On


   

Question 1184312: What is the co-efficient of 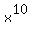+x%5E10+ in the following expressions:
(A) 1 + (1 + x) + (1 + x)^2 + ... + (1 + x)^20
(B) (1 + x)^2 + (1 + x)^3 + (1 + x)^4 + (1 + x)^5 + .... + (1 + x)^10
[Note: Here ^ means power]
Found 2 solutions by robertb, greenestamps:
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
(A)

=+%28sum%28%28matrix%282%2C1%2C21%2Ck%29%29%2Ax%5E%2821-k%29%2C+k=0%2C21%29+-+1%29%2Fx

=

(B) This should be more manageable than (A). Note that the term x%5E10 appears in the last term of the expression only, which is %281%2Bx%29%5E10.
Therefore the coefficient of x%5E10 is highlight%281%29

Answer by greenestamps(13198) About Me  (Show Source):
You can put this solution on YOUR website!


The second one is trivial; only the expansion of the last term in the sum contains an x^10 term, and the coefficient of that term is clearly 1.

(B) ANSWER: 1

In the first one, there is no x^10 term until we get to (1+x)^10. Then the coefficients of the x^10 terms in the expansion of the remaining terms in the given sum are...

(1+x)^10: C(10,10)
(1+x)^11: C(11,10)
(1+x)^12: C(12,10)
...
(1+x)^20: C(20,10)

The coefficient of the x^10 term in the sum is then found using the "hockey stick" equation for Pascal's Triangle:

C(10,10)+C(11,10)+C(12,10)+...+C(20,10) = C(21,11)

ANSWER: C(21,11) (which is the same as C(21,10))