Question 1183896: FInd the quadratic equation each of whose roots is the sum of a root and its reciprocal of the quadratic equation 2x^2 + 3x + 4 = 0.
Answer by ikleyn(52777)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
FInd the quadratic equation each of whose roots is the sum of a root
and its reciprocal of the quadratic equation 2x^2 + 3x + 4 = 0.
~~~~~~~~~~~~~~~~~~~
You are talking about another interpretation of the problem, previously solved.
This interpretation is slightly different problem, but still very close to the previous one.
It can be solved using the same method and metodology.
Again, this problem is to apply the Vieta's theorem several times.
Let " a " and " b " be the roots of the given equation.
Then according to Vieta's theorem, the sum (a+b) is equal to  : a + b = : a + b =  .
According to the same theorem, the product of the routs ab is equal to .
According to the same theorem, the product of the routs ab is equal to  = 2.
OK.
HENCE, the projected equation has the value A = = 2.
OK.
HENCE, the projected equation has the value A = 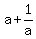 as one of its roots, and has the value B = as one of its roots, and has the value B = 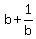 as the another root.
The sum of the roots A + B is A + B = as the another root.
The sum of the roots A + B is A + B =  = = 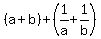 = = 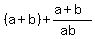 .
We substitute here a+b = .
We substitute here a+b =  and ab = 2, and we get A + B = and ab = 2, and we get A + B =  + +  = = 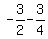 = = 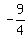 .
Next, A*B = .
Next, A*B = 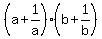 = = 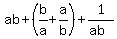 = 2 + = 2 + 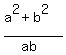 + +  = 2 = 2  + + 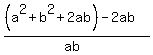 = 2 = 2  + + 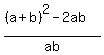 =
= 2 =
= 2  + + 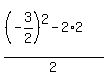 = 2 = 2  + + 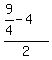 = 2 = 2  + +  = 2 = 2  - -  = =  - -  = = 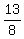 .
HENCE, applying the Vieta's theorem again, the projected equation has the form
x^2 - (A+B)x + AB = 0, or .
HENCE, applying the Vieta's theorem again, the projected equation has the form
x^2 - (A+B)x + AB = 0, or 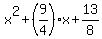 = 0.
You can have this equation with integer coefficient by multiplying its terms by 8. You will get then the final equation as = 0.
You can have this equation with integer coefficient by multiplying its terms by 8. You will get then the final equation as
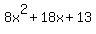 = 0. = 0.
Solved.
--------------
As I said, the same methodology works.
I think, that after my previous solution, an advanced student would be able to solve this one ON HIS OWN.
In any case, I am glad to hear your response, which was meaningful, what RARELY HAPPENS at this forum.
|
|
|