Question 1181712: A rocket is being launched vertically over a point 𝐴 on the ground with
a velocity of 550 𝑚𝑖Τℎ𝑟. Twenty five miles away from point 𝐴 on the
ground, there is a photographer video-taping the launch. At what rate
is the angle of elevation of the camera changing when the rocket
achieves an altitude of 25 miles?
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(2138)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to solve this related rates problem:
**1. Diagram and Variables:**
* Draw a right triangle.
* Point A is one vertex (where the rocket launches).
* The photographer is at another vertex, 25 miles away from A.
* The rocket's altitude is the vertical leg of the triangle (let's call it *y*).
* The distance from A to the photographer is the horizontal leg (25 miles).
* The angle of elevation from the photographer to the rocket is θ.
**2. Given Information:**
* dy/dt = 550 mi/hr (rocket's velocity)
* We want to find dθ/dt when y = 25 miles.
**3. Relate Variables:**
We can relate θ and y using the tangent function:
tan(θ) = y / 25
**4. Implicit Differentiation:**
Differentiate both sides of the equation with respect to time (t):
sec²(θ) * (dθ/dt) = (1/25) * (dy/dt)
**5. Solve for dθ/dt:**
dθ/dt = (1/25) * (dy/dt) / sec²(θ)
dθ/dt = (cos²(θ)/25) * (dy/dt)
**6. Find cos(θ) when y = 25 miles:**
When y = 25 miles, the triangle is a right isosceles triangle, so θ = 45 degrees or π/4 radians. Therefore, cos(θ) = cos(45°) = 1/√2.
**7. Substitute and Calculate:**
dθ/dt = ((1/√2)² / 25) * 550 mi/hr
dθ/dt = (1/50) * 550 mi/hr = 11 mi/hr
**8. Convert to radians per hour:**
Since angular velocity is typically expressed in radians per unit time, we need to convert miles/hour to radians/hour. The relationship between arc length (s), radius (r), and angle (θ in radians) is s = rθ. If we consider the distance from the observer to the launch point as the radius (25 miles), and the altitude of the rocket as the arc length (25 miles), then when the altitude is 25 miles, the angle of elevation is π/4 radians. The rate of change of the rocket's altitude is given in miles per hour. The rate of change of the angle of elevation will be in radians per hour.
When y = 25 miles, the angle of elevation is 45 degrees or π/4 radians.
dθ/dt = 11 miles/hour * (1 radian / 25 miles) = 0.44 radians/hour.
**Answer:** The angle of elevation is changing at a rate of 0.44 radians per hour when the rocket reaches an altitude of 25 miles.
Answer by ikleyn(53435)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A rocket is being launched vertically over a point 𝐴 on the ground with
a velocity of 550 𝑚𝑖/ℎ𝑟. Twenty five miles away from point 𝐴 on the
ground, there is a photographer video-taping the launch. At what rate
is the angle of elevation of the camera changing when the rocket
achieves an altitude of 25 miles?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution in the post by @CPhill is incorrect and his answer is incorrect, too.
The error is in the last step, where @CPhill converts the value of 11 mi/hr to radians/hr.
@CPhill mistakenly treats this value of 11 mi/hr as miles per hour.
Actually, it is 11 radians per hour, and conversion is just done on the way and IS NOT NEEDED anymore.
Below is my correct solution.
Here's how to solve this related rates problem:
**1. Diagram and Variables:**
* Draw a right triangle.
* Point A is one vertex (where the rocket launches).
* The photographer is at another vertex, 25 miles away from A.
* The rocket's altitude is the vertical leg of the triangle (let's call it *y*).
* The distance from A to the photographer is the horizontal leg (25 miles).
* The angle of elevation from the photographer to the rocket is θ.
**2. Given Information:**
* dy/dt = 550 mi/hr (rocket's velocity)
* We want to find dθ/dt when y = 25 miles.
**3. Relate Variables:**
We can relate θ and y using the tangent function:
tan(θ) = y / 25
**4. Implicit Differentiation:**
Differentiate both sides of the equation with respect to time (t):
sec²(θ) * (dθ/dt) = (1/25) * (dy/dt)
**5. Solve for dθ/dt:**
dθ/dt = (1/25) * (dy/dt) / sec²(θ)
dθ/dt = (cos²(θ)/25) * (dy/dt)
**6. Find cos(θ) when y = 25 miles:**
When y = 25 miles, the triangle is a right isosceles triangle, so θ = 45 degrees or π/4 radians. Therefore, cos(θ) = cos(45°) = 1/√2.
**7. Substitute and Calculate:**
dθ/dt = ((1/√2)² / 25) * 550 mi/hr
dθ/dt = (1/50) * 550 mi/hr = 11 radians/hr.
+-----------------------------------------------------------------------------+
| Conversion from mi/hr of the left side to radians/hr in the right side |
| is just made inside the previous formula. |
| This conversion is already built into the coefficients. |
+-----------------------------------------------------------------------------+
**Answer:** The angle of elevation is changing at a rate of 11 radians per hour when the rocket reaches an altitude of 25 miles.
Solved and answered correctly.
------------------------------
Post-solution note
11 radiance per hour is 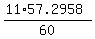 = 10.50423 degrees per minute, = 10.50423 degrees per minute,
if you want to have the answer in units that are adequate to the problem.
///////////////////////////////////////////////////////
This problem was posted to this forum several years ago (about 5 years ago).
It was solved by Edwin under this link
https://www.algebra.com/algebra/homework/quadratic/Quadratic_Equations.faq.question.1181710.html
https://www.algebra.com/algebra/homework/quadratic/Quadratic_Equations.faq.question.1181710.html
Edwin' solution was conceptually correct, but had an error in his implementation, leading to incorrect answer.
I found that solution via Google search, and placed there my corrected solution.
My solution follows to the Edwin's idea/design, but fixes/repairs that error.
Now both my solutions to this problem produce the same answer, bringing peace in your mind.
|
|
|