Question 1179834: The graph of a quadratic function passes through the origin and has
vertex (4, 16).
Use symmetry to identify one other point that must be on the graph of
this function.
Find an equation for this function.
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The graph of a quadratic function passes through the origin and has
vertex (4, 16).
Use symmetry to identify one other point that must be on the graph of
this function.
Find an equation for this function.
~~~~~~~~~~~~~
The other point is the point symmetrical to the origin point (0,0) relative to the axis of symmetry x=4 of the parabola.
This symmetrical point is 4 units to the right relative the symmetry line x=4,
and it has the same y-coordinate of 0.
So, the other point is (8,0).
The equation of the parabola in the vertex form is
y = 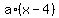 + 16. (1)
Since it is going through the origin point (x,y) = (0,0), from equation (1) we have
0 = + 16. (1)
Since it is going through the origin point (x,y) = (0,0), from equation (1) we have
0 = 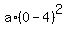 + 16, or
0 = 16a + 16
16a = -16,
a = + 16, or
0 = 16a + 16
16a = -16,
a = 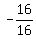 = -1.
Thus the equation of the parabola is
y = = -1.
Thus the equation of the parabola is
y = 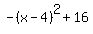 . .
 Plot y =
Plot y = 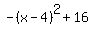 . .
Comparing my solution with that by @MathLover1, notice the difference:
the problem asks to find the point on the plot, symmetric to the origin of coordinates.
The origin of coordinates is the point (0,0), and the point symmetrical to it is the point (8,0), as I responded.
@MathLover1 considers totally different points, that are IRRELEVANT to the posed question.
|
|
|