Question 1177234: Determine the signs of the roots of the equation (if they exist) without solving the equation:

Found the discriminant (8)
But apparently the answer isn't 2 positive roots, so I'm stuck
Found 3 solutions by ankor@dixie-net.com, MathLover1, ikleyn:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Determine the signs of the roots of the equation (if they exist) without solving the equation:

The discriminant

4 + 4 = 8
Positive means two distinct real roots, not necessarily both positive
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! using the Descartes' Rule of Signs
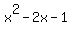 ....look for changes in sine ....look for changes in sine
So, the coefficients are  , , , , . .
As can be seen, there is  change. change.
This means that there is  positive real root. positive real root.
Replace  by by 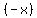 : :

The coefficients are  , , , , . .
As can be seen, there is  change. change.
This means that there is  negative real root. negative real root.
The discriminant determines the nature of the roots of a quadratic equation. The word 'nature' refers to the types of numbers the roots can be — namely real, rational, irrational or imaginary.
If the discriminant is positive, we know that we have  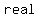 solutions that could be both positive, both negative, or one solution is positive and other is negative solutions that could be both positive, both negative, or one solution is positive and other is negative
so,  =>discriminant is positive, we know that we have =>discriminant is positive, we know that we have  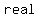 solutions solutions
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The discriminant of the equation d = b^2 - 4ac = (-2)^2 + 4*1*(-1) = 4 + 4 = 8 is a positive real number,
so the roots are real numbers.
Next, according to the Vieta's theorem, the product of the roots is equal to the constant term, which is -1 in this case,
so the roots are of opposite signs: one root is a positive real number, while another root is a negative real number.
That's all.
Solved, answered, explained and completed.
|
|
|