Question 1176694: Vertex (1,3); passing through (2,6)
Found 2 solutions by Solver92311, math_tutor2020:
Answer by Solver92311(821)   (Show Source):
You can put this solution on YOUR website!
Rules for posting on this website:
1. Ask an actual question. A question is a series of words that form a sentence where it is appropriate to append a question mark,
(i.e., one of these things: "?") to the end of the sentence.
Please look up the definition if you are still unclear on the concept.
On this website, such a question should relate to some area of mathematics.
2. If you post a problem for which you want a solution, make sure you make it clear what it is about the problem that is giving you difficulty.
3. Show all of the work, successful or not, done or attempted in the solution of the problem. In other words, demonstrate that you are trying to learn something about mathematics as opposed to just trying to get someone else to do your thinking for you.
4. If following these instructions is too much work for you, then helping you is too much work for us.
John
My calculator said it, I believe it, that settles it
From
I > Ø
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
Recall that
represents the generalized vertex form.
a = leading coefficient
h = x coordinate of vertex
k = y coordinate of vertex
Since the vertex given to us is (1,3), this means (h,k) = (1,3)
In other words,
h = 1
k = 3
We're also told the parabola passes through (x,y) = (2,6)
x = 2
y = 6
We have these four items of info
h = 1
k = 3
x = 2
y = 6
Plug those four items into the first equation mentioned and isolate 'a'.
The leading coefficient is positive, so the parabola opens upward.
We have
turn into
after plugging in a = 3, h = 1, k = 3
We could expand things out and combine like terms like so
 FOIL rule
 Distribute
 Combine like terms
The vertex form expands and simplifies to the standard form
Graph:
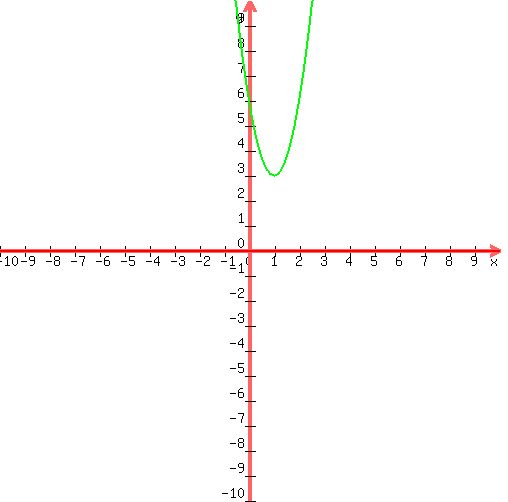
note the vertex is the lowest point at (1,3)
|
|
|
