Question 1166998: Horatio, a local farmer and part time magician, wants to create a rectangular compound for his chickens using wire fencing. Furthermore, he needs to divide the compound into two rectangular pens, to separate the roosters from the hens, by installing a dividing fence in the middle. He has 450 meters of fence. Determine the dimensions maximizing the enclosed area. What is the maximum area?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! he needs to divide the compound into two rectangular pens, to separate the roosters from the hens, by installing a dividing fence in the middle.
He has 450 meters of fence.
Determine the dimensions maximizing the enclosed area.
let L = the length of the compound
Let w = the width
:
2L + 3w = 450, w has two sides and the dividing fence
2L = (450-3w)
divide by 2
L = (225-1.5w)
:
A = L * w
Replace L with (225-1.5w)
A = w(225-1.5w)
A = 225w - 1.5w^2
a quadratic equation
-1.5w^2 + 225w = 0
max area occurs on the axis of symmetry, x=-b/(2a), which is
w = 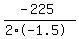
w = 75 ft is the width of max area
then
L = 225 - 1.5(75)
L = 225 - 112.5
L = 112.5 ft is the length of max area
:
What is the maximum area?
112.5 * 75 = 8,437.5 sq/ft
:
|
|
|