Question 1162659: The Extreme Rock Climbing Club planned a climbing expedition. The total cost was $1600, which was to be divided equally among the members going. Prior to the trip, 15 members decided not to go. If the cost per person increased by $24, how many people went on the expedition?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52778)   (Show Source):
You can put this solution on YOUR website! .
Let n = "how many people went on the expedition" (the number under the question).
Then the number of members PRIOR the trip was n+15.
The problem says
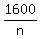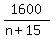 -  = 24.
Simplify step by step and solve for n
1600*(n+15) - 1600*n = 24n*(n+15)
1600*15 = 24n*(n+15)
1000 = n*(n+15) (*)
The solution to equation (*) (which can be EASILY guessed MENTALLY) is n = 25.
If you want to solve the problem formally, you can solve the quadratic equation (*) by any way you can/(you want).
ANSWER. 25 members went on the expedition.
Solved.
-------------
If you are seriously intended to learn Algebra, please read the following very attentively.
This problem belongs to a special class of problems.
Similar problems for Travel and Distance are often solved using the "Time" equation.
There are special lessons in this site written by me to teach students solving such problems.
See the links below . . .
Another similar problems belong to the set of problems "Had they sold their items in different way . . . "
There is a special lesson in this site written by me to teach students solving such problems, too.
See the link below . . .
I am not sure if this set of problems is covered in the standard US middle school/high school curriculum.
Surely, these problems are NOT for beginners studying Algebra.
They are intended for advanced and self-standing students, looking outside the box and interested in developing their skills.
Regarding myself, I learned about the methods of their solutions not from my school curriculum -
- for it, I read popular books in Math; popular brochures; preparation books on Math for entering university;
books related to Math circles and so on.
What I can say for sure is THIS: if you don't know the methods on how to setup such problems;
if you don't know the methods to deduce them from wording form to equations - then you are POWERLESS to solve them.
The guessing method, as I often repeat it many times (joking) - works good only if you know the solution in advance.
Therefore, learn these methods from my posts without looking (regardless) on how the tutor @greenestamps comments them.
Otherwise, you will know NOTHING.
In other words, otherwise you will not know the subject.
Otherwise, you even will not know where to start . . .
~~~~~~~~~~~~~~~~~
And finally, below are the promised links to the mentioned lessons.
- Had a car move faster it would arrive sooner
- How far do you live from school?
- Earthquake waves
- Time equation: HOW TO use, HOW TO write and HOW TO solve it
- Had they sold . . .
Answer by greenestamps(13198)  (Show Source):
You can put this solution on YOUR website!
Especially if this is a problem from a beginning algebra class, then you should know how to set up and solve the problem using formal algebra.
However, the whole problem can be solved mentally, if an algebraic solution is not required, and if you are good with mental arithmetic.
You only need to find two ways to write 1600 as the product of two positive integers which satisfy the conditions of the problem.
The first four pairs that I find are these:
40 * 40 = 1600
80 * 20 = 1600
64 * 25 = 1600
32 * 50 = 1600
You are looking for any two numbers in that list that differ by 24; 64 and 40 satisfy that requirement. And the corresponding numbers 40 and 25 differ by 15, which satisfies the other condition. So these are the numbers you are looking for.
ANSWER:
Originally, 40 members were going to go, paying $40 each. When 15 members backed out, 25 members paid $64 each -- an increase of $24.
|
|
|
