Question 1162180: determine k such that g(x)=3x^2+8x+k intersects f(x)=2x-1 at ine point.
Found 2 solutions by Boreal, ikleyn:
Answer by Boreal(15235)   (Show Source):
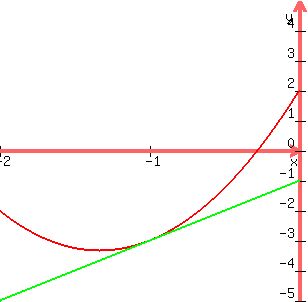
You can put this solution on YOUR website! find a place where the line 2x-1 is tangent to the curve.
Want one point only, where the slopes are the same, 2, because that is the slope of the line
find slope of the quadratic: derivative is 6x+8, and that equals 2 when x=-1
when x=-1, 2x-1=-3
so the point is (-1, -3) for the line. It has to be for the quadratic as well.
when x=-1, the quadratic is 3-8+k and that has to equal -3
-5+k=-3
k=2
Answer by ikleyn(52778)  (Show Source):
You can put this solution on YOUR website! .
They want you find the value of "k" in a way that the straight line f(x) = 2x-1 be a tangent line
to the parabola g(x) = 3x^2 + 8x + k.
It means that the equation
3x^2 + 8x + k = 2x - 1
has only one real root (the two roots merge into one root).
The equation is equivalent to
3x^2 + 6x + (k+1) = 0. (*)
Its discriminant is
b^2 - 4ac = 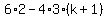 = 36 - 12(k+1)
We want the discriminant be zero
36 - 12(k+1) = 0, or 36 = 12(k+1), k+1 = 36/12 = 3, k = 3-1 = 2.
ANSWER. k = 2.
CHECK. At k= 2, the equation (*) becomes 3x^3 +6x + 3 = 0.
It is equivalent to x^2 + 2x + 1 = 0, which factors into  = 0 and has only one real solution x= -1.
The point (x,f(x)) = (-1,f(-1)) = (-1,-3) is the same as the point (x,g(x)) = (-1,g(-1)) = (-1,-3).
It is the unique common point of the two given lines.
Solved. // The problem was solved using Algebra only, without using Calculus.
|
|
|
