SOLUTION: Joe Klothes has determined that the profit function for selling x thousand pairs of shorts is P(x)= -5x^2+19x-12 a) How many pairs of shorts must the company sell to break even?

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: Joe Klothes has determined that the profit function for selling x thousand pairs of shorts is P(x)= -5x^2+19x-12 a) How many pairs of shorts must the company sell to break even?      Log On


   

Question 1158572: Joe Klothes has determined that the profit function for selling x thousand pairs of shorts is P(x)= -5x^2+19x-12
a) How many pairs of shorts must the company sell to break even?
b) How many pairs of shorts must the company sell to be profitable?
c)HOw many pairs of shorts must the company sell to maximize profits?
Answer by Shin123(626) About Me  (Show Source):
You can put this solution on YOUR website!
Solved by pluggable solver: Completing the Square for Quadratics
To complete the square for the quadratic -5%2Ax%5E2%2B19%2Ax-12=0, we must first find a square which when expanded, has -5x2 and 19x in it.
Factoring -5 from the left side gives 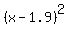-5%28x%5E2-3.8%2Ax%2B2.4%29=0. %28x-1.9%29%5E2 is the square we are looking for. So we get -5%28%28x-1.9%29%5E2-1.21%29=0. Taking the -1.21 out of the -5, we get highlight%28-5%28x-1.9%29%5E2%2B6.05%29. Subtracting 6.05 from both sides, we get -5%28%28x-1.9%29%5E2%29=-6.05. Since the right side is negative, there are no real solutions.

a) They must sell 3,000 or 800 pairs of shorts to break even.
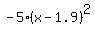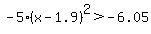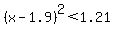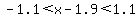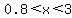b) To be profitable, the expression -5%28x-1.9%29%5E2 must be greater than -6.05. -5%28x-1.9%29%5E2%3E-6.05. 5%28x-1.9%29%5E2%3C6.05. %28x-1.9%29%5E2%3C1.21. -1.1%3Cx-1.9%3C1.1. 0.8%3Cx%3C3. They must sell a number of pants between 800 and 3,000 to be profitable.
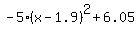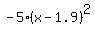c) To maximize profit, the expression -5%28x-1.9%29%5E2%2B6.05 need to be at its maximum. The square of any real number is nonnegative. the expression is maximized when -5%28x-1.9%29%5E2 is 0. This occurs when x=1.9. They must make 1,900 pairs of pants to maximize profit.