SOLUTION: A roofer thows a group of shingles into the trash bin on the ground below. The height of the shingles can be modeled by the function h(t)= -5t^2+11t+12 where h(t) is the height in

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: A roofer thows a group of shingles into the trash bin on the ground below. The height of the shingles can be modeled by the function h(t)= -5t^2+11t+12 where h(t) is the height in      Log On


   

Question 1158571: A roofer thows a group of shingles into the trash bin on the ground below. The height of the shingles can be modeled by the function h(t)= -5t^2+11t+12 where h(t) is the height in meters and t is the time in seconds
a) how long will it take the shingles to hit the bottom of the trash?
b) Determine the maximum height of the shingles?
Thank you
Answer by Shin123(626) About Me  (Show Source):
You can put this solution on YOUR website!
Solved by pluggable solver: Completing the Square for Quadratics
To complete the square for the quadratic -5%2Ax%5E2%2B11%2Ax%2B12=0, we must first find a square which when expanded, has -5x2 and 11x in it.
Factoring -5 from the left side gives 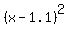-5%28x%5E2-2.2%2Ax-2.4%29=0. %28x-1.1%29%5E2 is the square we are looking for. So we get -5%28%28x-1.1%29%5E2-3.61%29=0. Taking the -3.61 out of the -5, we get highlight%28-5%28x-1.1%29%5E2%2B18.05%29. Subtracting 18.05 from both sides, we get -5%28%28x-1.1%29%5E2%29=-18.05. Since the right side is negative, there are no real solutions.

Since time can't be negative, it takes 3 seconds for the shingles to hit the trash. The maximum value occurs when -5%28x-1.1%29%5E2 is 0. This happens when x=1.1. The maximum height is 18.05 meters and it occurs after 1.1 seconds has passed.