SOLUTION: A quadratic equation has roots {{{a}}} and {{{b}}}. If {{{a+b=6}}} and {{{a-b=4}}}, find an expression for the equation in the form {{{ax^2+bx+c}}}.

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: A quadratic equation has roots {{{a}}} and {{{b}}}. If {{{a+b=6}}} and {{{a-b=4}}}, find an expression for the equation in the form {{{ax^2+bx+c}}}.      Log On


   

Question 1146313: A quadratic equation has roots a and b.
If a%2Bb=6 and a-b=4, find an expression for the equation in the form ax%5E2%2Bbx%2Bc.
Answer by math_helper(2461) About Me  (Show Source):
You can put this solution on YOUR website!
A quadratic equation has roots a and b.
If a%2Bb=6 and a-b=4, find an expression for the equation in the form ax%5E2%2Bbx%2Bc.
-------------

I like this formulation better:
A quadratic equation has roots a and b.
If a%2Bb=6 and a-b=4, find an expression for the equation in the form Ax%5E2%2BBx%2BC. Note that A,B, and C are not the same as a,b
----
a+b = 6, a-b = 4 tells you a=5, b=1
Thus, (x-5)(x-1) = 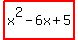highlight%28+x%5E2-6x%2B5+%29 is the quadratic (A=1, B=-6, C=5, in agreement with Viete's Theorem)