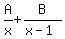1. (a) resolve into partial fractions 2x/[(x-2)(x+5)]
(b) resolve into partial fractions 1/(x^2-x)
1. (a) resolve into partial fractions 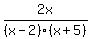 The other person’s solution: A =
The other person’s solution: A =  , and B =
, and B =  , is WRONG!!
, is WRONG!!
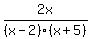 =
= 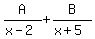
 ---- Multiplying by LCD, (x - 2)(x + 5)
2x = A(x + 5) + B(x - 2) ---- Equating NUMERATORS, since denominators are the same
2(2) = A(2 + 5) + B(2 - 2) ---- Substituting 2 for x to determine the value of A
4 = 7A
---- Multiplying by LCD, (x - 2)(x + 5)
2x = A(x + 5) + B(x - 2) ---- Equating NUMERATORS, since denominators are the same
2(2) = A(2 + 5) + B(2 - 2) ---- Substituting 2 for x to determine the value of A
4 = 7A
 2(- 5) = A(- 5 + 5) + B(- 5 - 2) ---- Substituting - 5 for x to determine the value of B
- 10 = - 7B
2(- 5) = A(- 5 + 5) + B(- 5 - 2) ---- Substituting - 5 for x to determine the value of B
- 10 = - 7B
 (A, B) = (
(A, B) = ( ,
, 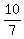 )
Therefore,
)
Therefore, 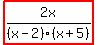 =
= 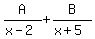 =
=  1. (b) resolve into partial fractions
1. (b) resolve into partial fractions 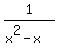 Use the same concept above, to decompose this PROPER FRACTION too.
Before doing so though, we FACTORIZE the denominator in
Use the same concept above, to decompose this PROPER FRACTION too.
Before doing so though, we FACTORIZE the denominator in 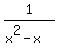 to get:
to get: 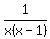 , and then:
, and then: 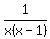 =
=