SOLUTION: Find the values of a for which the curve y= x^2 never touches the curve y= a-(x-a)^2

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: Find the values of a for which the curve y= x^2 never touches the curve y= a-(x-a)^2      Log On


   

Question 1143176: Find the values of a for which the curve y= x^2 never touches the curve y= a-(x-a)^2
Answer by MathLover1(20849) About Me  (Show Source):
You can put this solution on YOUR website!
Find the values of a for which the curve y=+x%5E2 never touches the curve y=+a-%28x-a%29%5E2+
y=+x%5E2+
y=+a-%28x-a%29%5E2
------------------------
x%5E2+=a-%28x-a%29%5E2
x%5E2+=a-%28x%5E2-2xa%2Ba%5E2%29
x%5E2+%2B%28x%5E2-2xa%2Ba%5E2%29-a=0
x%5E2+%2Bx%5E2-2xa%2Ba%5E2-a=0
2x%5E2-2ax%2Ba%5E2-a=0
use discriminant D=b%5E2-4ac+
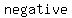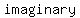When a,+b, and c are real numbers, a+%3C%3E+0 and discriminant is negative, then the roots α and β of the quadratic equation ax%5E2+%2B+bx+%2B+c+=+0+are unequal and not real. In this case, we say that the roots are imaginary.
in your case discriminant D is:
2x%5E2-2ax%2Ba%5E2-a=0
since a=2,+b=-2a, and c=a%5E2-a
D=%28-2a%29%5E2-4%2A2%28a%5E2-a%29
D=4a%5E2-8%28a%5E2-a%29
D=4a%5E2-8a%5E2%2B8a
D=-4a%5E2%2B8a
D=-4a%28a-2%29

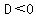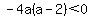
if D%3C0 => -4a%28a-2%29%3C0
solutions:
if 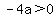-4a+%3E0 =>a%3C0
if 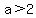%28a-2%29%3E0=>a%3E2

so, your solution is:
a is in interval (-infinity, 0)
or
a is in interval (2,infinity)


check some values:
let's a=-1 in interval (-infinity, 0)
y=+x%5E2+
y=+-1-%28x%2B1%29%5E2
graph:
+graph%28+600%2C+600%2C+-10%2C10%2C+-10%2C+10%2C+x%5E2%2C-1-%28x%2B1%29%5E2%29+
so, the curve y=+x%5E2 never touches the curve y=+a-%28x-a%29%5E2

let's a=3 in interval (2,infinity)
y=+x%5E2+
y=+3-%28x-3%29%5E2
graph:
+graph%28+600%2C+600%2C+-10%2C10%2C+-10%2C+10%2C+x%5E2%2C3-%28x-3%29%5E2%29+
so, the curve y=+x%5E2 never touches the curve y=+a-%28x-a%29%5E2