SOLUTION: Given that x²+bx+18 is factorised as (x+2)(x+c). Find the values of c and b

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: Given that x²+bx+18 is factorised as (x+2)(x+c). Find the values of c and b      Log On


   

Question 1142263: Given that x²+bx+18 is factorised as (x+2)(x+c). Find the values of c and b
Found 3 solutions by josgarithmetic, ikleyn, Alan3354:
Answer by josgarithmetic(39616) About Me  (Show Source):
Answer by ikleyn(52776) About Me  (Show Source):
You can put this solution on YOUR website!
.
Since x^2 + bx + 18 is factored as (x+2)*(x+c), it means that x= -2 is the root of the polynomial x^2 + bx + 18 :


    (-2)^2 + b*(-2) + 18 = 0,

    4       -2b     + 18 = 0,

    4 + 18 = 2b  ====>  2b = 22  ====>  b = 11.



Next, according to Vieta's theorem, the constant term 18 of the polynomial x^2 + bx + 18  is the product of its roots.


One of the root is x= -2.  Hence, the other root is 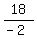 18%2F%28-2%29 = -9.

From the other side, the other root is x= -c.  

Hence,  c= 9.


ANSWER.  b = 11;  c = 9.

Solved.



Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
Given that x²+bx+18 is factorised as (x+2)(x+c). Find the values of c and b
------------
c = 18/2 = 9 ---- Could that be more obvious?
---> b = 2 + 9 = 11