Question 113995This question is from textbook Introductory and Intermediate Algebra
: The Hudson River flows at a rate of 3mph. A patrol boat travels 60 miles upriver and returns in a total time of 9 hr. What is the speed of the boat in still water?
D= rt upriver - 9r = 60 still water - 3rt = 60
Have I set this equation up correctly? Where do I go from here? Please help me.
This question is from textbook Introductory and Intermediate Algebra
Found 2 solutions by jim_thompson5910, checkley71:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let r=speed of the boat in still water
When the boat goes upstream, we subtract 3mph from r to get (the boat is slowed by 3mph)

When the boat goes downstream, we can add 3mph to r to get (the boat is sped up by 3mph)

Now since the distance is the same we can set the two equations equal to one another to get
 Now solve for Now solve for  in the first equation in the first equation
 Now solve for Now solve for  in the second equation in the second equation
Since the total time was 9 hr, this means 
 Plug in Plug in  and and 
 multiply by the LCD multiply by the LCD 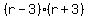
 Distribute Distribute
 Foil Foil
 Distribute again Distribute again
 Combine like terms Combine like terms
 Subtract 120r from both sides Subtract 120r from both sides
 Rearrange the terms Rearrange the terms
Now let's use the quadratic formula to solve for r:
Starting with the general quadratic

the general solution using the quadratic equation is:

So lets solve  ( notice ( notice  , ,  , and , and  ) )
 Plug in a=9, b=-120, and c=-81 Plug in a=9, b=-120, and c=-81
 Negate -120 to get 120 Negate -120 to get 120
 Square -120 to get 14400 (note: remember when you square -120, you must square the negative as well. This is because Square -120 to get 14400 (note: remember when you square -120, you must square the negative as well. This is because  .) .)
 Multiply Multiply  to get to get 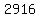
 Combine like terms in the radicand (everything under the square root) Combine like terms in the radicand (everything under the square root)
 Simplify the square root (note: If you need help with simplifying the square root, check out this solver) Simplify the square root (note: If you need help with simplifying the square root, check out this solver)
 Multiply 2 and 9 to get 18 Multiply 2 and 9 to get 18
So now the expression breaks down into two parts
 or or 
Now break up the fraction
 or or 
Simplify
 or or 
So these expressions approximate to
 or or 
So our possible solutions are:
 or or 
However, we cannot have a negative speed, so our only solution is 
So the speed of the boat in still water is about 13.977 mph
Answer by checkley71(8403)   (Show Source): (Show Source):
You can put this solution on YOUR website! D=RT OR T=D/R
60/(R-3)+60/(R+3)=9
[60(R+3)+60(R-3)]/(R-3)(R+3)=9
(60R+180+60R-180)/(R^2-9)=9 (THE +180 & THE -180 CANCEL OUT)
120R/(R^2-9)=9 NOW CROSS MULTIPLY
9R^2-81=120R
9R^-120R-81=0
USING THE QUADRATIC EQUATION WE GET:

R=(120+-SQRT[120^2-4*9*-81])/2*9
R=(120+-SQRT[14,400+2916])/18
R=(120+-SQRT17,316)/18
R=(120+-131.59)/18
R=(120+131.59)/18
R=251.59/18
R=13.977 MPH IS THE SPEED OF THE BOAT IN STILL WATER.
|
|
|