Question 113700: Starting with ax2 + bx + c = 0 and show each step to end up with:
x = - b + √b2 - 4ac
_______________________
2a
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! Quadratic Formula Proven

Consider equation in a standard form 
. What we want to do is complete the square, that is; note that  , ,  , and , and  can be positive as well as negative. The right part of the equation should can be positive as well as negative. The right part of the equation should 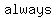 be be  . .
get an equation like this:
(...)^2 = ...
Divide both parts by  : :

 ………..we will ………..we will 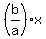 multiply and divide by multiply and divide by 
 ………..move ………..move  to the right to the right
 ……….. ………..
Now, if we want to 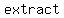   of a of a  out of here, we can out of here, we can 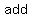 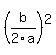 to both sides of the equation: to both sides of the equation:
 ……….. ………..
We did it so that the formula to the left would be a complete square of an expression:
 ……….. ………..
On the left side, there is a square of something, on the right, it is a number.
As you know, for all real numbers their squares are 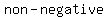 . .
So if the number to the right happens to be 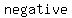 , this means that , this means that  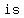   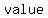   that would satisfy this equation. that would satisfy this equation.
That's where the discriminat rule comes from.
Since the roots of equations like  are are  , we have: , we have:

This quadratic formula can be simplified as:
open the bracket with  : :


divide and multiply the square root by  : :

get  inside the square root as inside the square root as  : :

use distributive property:

Simplify:

Or

get 2a as the common denominator:

|
|
|