Question 1132198: The Johnson High school theater club is trying to set the price of tickets for a play.If the price is too low,they will not make enough money to cover expenses and if the price is too high,not enough people will pay the price of a ticket.They estimate that their total income per concert,I,in hundreds of dollars,can be approximated by the formula
I=-x^2+24x-44,0 ≤ x ≤ 24 where x is the cost of a ticket
a)draw the graph of income versus the cost of a ticket.
b)Determine the minimum cost of a ticket for the theater club to break even.
c)Determine the maximum cost of a ticket that the theater club can charge and break even.
d)How much should they charge to receive maximum income?
e)Find the maximum income.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the graph is shown below:
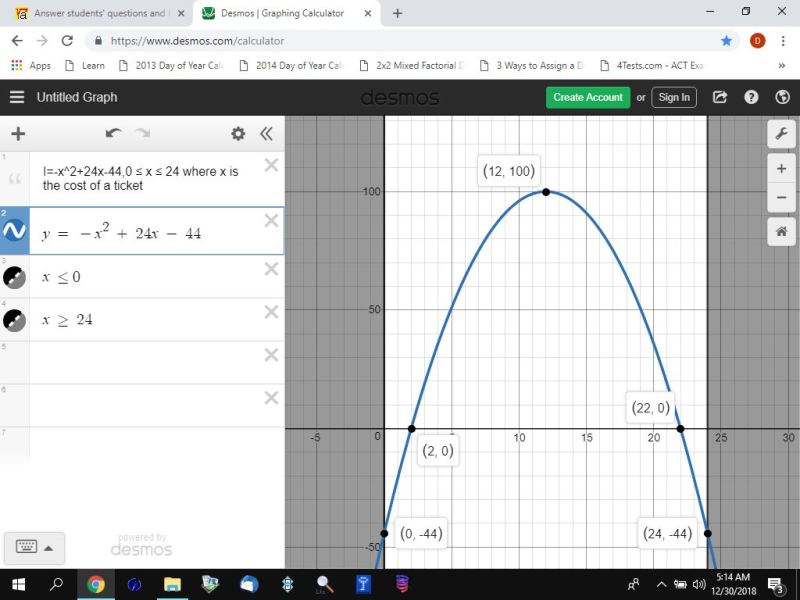
x represents the price of a ticket.
y represents the income.
from the graph, it can be seen that:
when the cost of a ticket is 0 dollars, they will lose 44 dollars.
when the cost of a ticket is 2 dollars, they will break even.
when the cost of a ticket is 12 dollars, they will make 100 dollars.
when the cost of a ticket is 22 dollars, they will break even.
when the cost of a ticket is 24 dollars, they will lose 44 dollars.
answers to the questions are shown below:
a)draw the graph of income versus the cost of a ticket.
done - see above.
b)Determine the minimum cost of a ticket for the theater club to break even.
2 dollars
c)Determine the maximum cost of a ticket that the theater club can charge and break even.
22 dollars
d)How much should they charge to receive maximum income?
12 dollars
e)Find the maximum income.
100 dollars
the break even income can also be found by factoring the quadratic equation.
the maximum income can also be found by finding the value of x = -b/2a and then evaluating the equation with that value of x.
the equation is y = -x^2 + 24x - 44.
to factor, do the following:
set y equal to 0 to get -x^2 + 24x - 44 = 0
multiply both sides by -1 to get (-1) * (x^2 - 24x + 44) = 0
factor x^2 - 24x + 44 to get (x - 2) * (x - 22)
the equation becomes (-1) * (x - 2) * (x - 22) = 0
the equation will be equal to 0 when x = 2 or when x = 22 or when x = 2 and x = 22.
to find the maximum income, do the following:
place the equation in standaed form of y = -x^2 + 24x - 44
when in this form:
a = coefficient of the x^2 term = -1
b = coefficient of the x term = + 24
c = constant term = -44
the maximum income will be at x = -b/2a = -24/-2 = 12
the maximum income will be -12^2 + 24*12 - 44 = 100
note that -12^2 is equal to - (12^2) and not equal to (-12)^2.
the value that's being square is the 12, not the -12.
the graph confirms that the maximum value is at x = 12.
the graph confirms that the income is 0 when x = 2 and when x = 22.
the graph confirms that the school loses 44 dollars when x = 0 and when x = 24.
|
|
|