SOLUTION: Factor fully (2m-3)^2-(8m^2-4)^2

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: Factor fully (2m-3)^2-(8m^2-4)^2      Log On


   

Question 1131329: Factor fully (2m-3)^2-(8m^2-4)^2
Found 3 solutions by MathLover1, MathTherapy, ikleyn:
Answer by MathLover1(20849) About Me  (Show Source):
Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!
Same as: Quadratic_Equations/1131330: 

Again, you don't need to FOIL the BINOMIALS.

Again, this is a DIFFERENCE of TWO SQUARES <======> matrix%281%2C3%2C+a%5E2+-+b%5E2%2C+%22=%22%2C+%28a+-+b%29%28a+%2B+b%29%29

The same concept applies!!

Correct answer: highlight_green%28%28-+4m+-+1%29%282m+-+1%29%288m%5E2+%2B+2m+-+7%29%29

Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
(2m-3)^2 - (8m^2-4)^2.


     Use the general formula  a%5E2 - b%5E2 = (a+b)*(a-b), which is valid for any numbers "a" and "b".

     In this case,  a = (2m-3),  b = 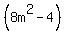%288m%5E2-4%29,  so


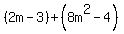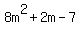     a + b = %282m-3%29+%2B+%288m%5E2-4%29 = 8m%5E2+%2B+2m+-+7.

     a - b = %282m-3%29+-+%288m%5E2-4%29 = -8m%5E2+%2B+2m+%2B1 = -(2m-1)*(4m+1).


Therefore,

(2m-3)^2 - (8m^2-4)^2 = -%288m%5E2+%2B+2m+-+7%29%2A%282m-1%29%2A%284m%2B1%29.      ANSWER

Solved.

--------------------

The key idea and the lesson to learn is THIS : 

     Use the formula  a%5E2 - b%5E2 = (a+b)*(a-b).

And there is nothing interesting after that - only the mechanical work.