SOLUTION: A vacant lot is being converted into a community garden. The garden and the walkway around its perimeter have an area of 238 ft2. Find the width of the walkway if the garden is 12

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: A vacant lot is being converted into a community garden. The garden and the walkway around its perimeter have an area of 238 ft2. Find the width of the walkway if the garden is 12       Log On


   

Question 1124406: A vacant lot is being converted into a community garden. The garden and the walkway around its perimeter have an area of 238 ft2. Find the width of the walkway if the garden is 12 ft wide by 15 ft long.
*I am not sure where I am going wrong. I've set the problem to zero and then plugged each variable into the quadratic formula. However, the answer I keep getting when I go to confirm the solution is wrong.*
Answer by ikleyn(52784) About Me  (Show Source):
You can put this solution on YOUR website!
.
.
The problem assumes that the walkway has a uniform width.


1.   The easy way to solve it MENTALLY 

The difference the length minus the width of the garden is  15 - 12 = 3 ft.


Since the walkway is of uniform width, the difference between the length and the width of the large rectangle
    must be the same 3 ft.


So we need to find a decomposition of the number 238 (238 sq.ft., the area) into the product of two numbers with 
   the difference of 3 between them.


As soon as you re-formulated the problem in this way, you can guess the answer MENTALLY and MOMENTARILY: 
    the numbers are 14 and 17.

    238 = 2*119 = 2*7*17 = 14*17.


Answer.  The dimensions of the large rectangle are 14 and 17 feet.

         The uniform width of the border is 1 ft.  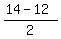( = %2814-12%29%2F2 = %2817-15%29%2F2. )


2.   Formal algebra solution 

Let x be the uniform walkway width.

Then the dimensions of the larger rectangle are (15+2x)  and  (12+2x) feet.


So the area of the large rectangle is

(15+2x)*(12+2x) = 238.


It is your equation to find the unknown x.


Simplify it; write as a quadratic equation in standard form and solve by using the quadratic formula or factoring.

-------------------

If you want to see many other similar solved problems, look into the lessons
    - Problems on the area and the dimensions of a rectangle surrounded by a strip
    - Cynthia Besch wants to buy a rug for a room
in this site.

Also,  you have this free of charge online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

The referred lesson is the part of this online textbook under the topic
"Dimensions and the area of rectangles and circles and their elements".

Save the link to this online textbook together with its description

Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson

to your archive and use it when it is needed.