SOLUTION: A real estate company owns 228 efficiency apartments, which are fully occupied when the rent is $990 per month. The company estimates that for each $25 increase in rent, 5 apartmen

The condition says "for each $25 increase in rent, 5 apartments will become unoccupied".


It is the same as (is equivalent) to say that for each $5 increase in rent, 1 apartment will become unoccupied.


So inter-relation between the number of occupied apartments "n" and the rent cost "p" (payment, in dollars) is THIS :


    if the price is  p(m) = 990 + 5m,  then the number of occupied apartments is n = 228 - m,  where "m" is an integer number (a parameter).


It means that the revenue is

    R(m) = p*n = p(m)*n(m) = (990 + 5m)*(228-m).


It is a quadratic function of m.  It is more convenient to present it as the quadratic function of the real argument x


    R(x) = {990 + 5x)*(228-x).


This quadratic function, obviously, is open downward (has negative coefficient at x^2); so, it has maximum, and our goal is to find this maximum.


Note that the roots of this quadratic polynomial are easy to find by equating each factor to zero.

It gives the zeroes  x = 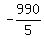 = -198  and  x = 228.


The maximum of the quadratic function is achieved exactly mid-way between the zeroes - so the maximum is at  x= 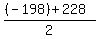 = 15.


It means that the optimal price is  p(m) = p(15) = 990 + 5m = 990 + 5*15 = 1065 dollars,

which provides the number of occupied apartments  n(m) = n(15) = 228 - m = 228 - 15 = 213.


Then the revenue is  213*1065 =  226845 dollars.


Compare it with the revenue at full occupancy:  228*990 = 225720 dollars.