Question 1122448: problem solving using quadratic functions:
Assume the perimeter of a rectangle is P and that the area is to be maximized. Let x represent the width of the rectangle. Using quadratic functions, show that the rectangle must be a square.
Found 2 solutions by ikleyn, htmentor:
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! A rectangle with a given perimeter which has the maximal area is a square
There are many rectangles with a given perimeter.
For example, if the perimeter is 200 feet, you can consider rectangles 20 by 80 feet, 30 by 70 feet, 40 by 60 feet, 50 by 50 feet and many others.
The amazing fact is: among rectangles with a given perimeter, a square has the maximal area.
TheoremAmong rectangles with a given perimeter, a square has the maximal area.
Proof
Let P be the given perimeter of a rectangle, and let L be the length and W be the width of the rectangle.
Then we have
2L + 2W = P,
so we can express W as
W = 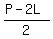 .
The area of the rectangle is
L*W = .
The area of the rectangle is
L*W = 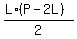 = = 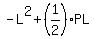 . .
Now let me remind you that, if you have a quadratic function f(x) =  of the general form,
then it reaches the maximum/minimum at x = of the general form,
then it reaches the maximum/minimum at x = 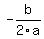 . . |
See the lessons
- HOW TO complete the square to find the minimum/maximum of a quadratic function
- Briefly on finding the minimum/maximum of a quadratic function
in this site.
For our situation, L = 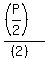 = = 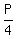 .
Then W = .
Then W = 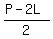 = = 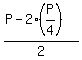 = = 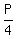 ,
and the rectangle is the square with L = W = ,
and the rectangle is the square with L = W = 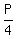 .
The statement is proved. .
The statement is proved.
Let me repeat the statement one more time:
Among rectangles with a given perimeter P, a square with the side length 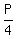 has the maximal area, which is equal to has the maximal area, which is equal to 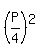 . .
|
Example 1A rectangle has a perimeter of 100 meters. What are the dimensions of the sides if the area is a maximum?
Solution
According to the proved statement above, the rectangle is a square with the side length of 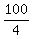 = 25 meters. = 25 meters.
Problem 1A piece of wire 20 inches long is to be cut into a rectangle. How long should each side of the rectangle be to maximize the area of the rectangle?
Solution
According to the proved statement above, the rectangle should be a square with the side length of  = 5 inches. = 5 inches.
Problem 2A farmer has 280 feet of fence to enclose a rectangular garden. What dimensions for the garden give the maximum area?
Solution
According to the proved statement above, the rectangular garden should be a square with the side length of 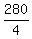 = 70 feet. = 70 feet.
----------------
What you see in this post, is the lesson
- A rectangle with a given perimeter which has the maximal area is a square
from this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic "Finding minimum/maximum of quadratic functions".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by htmentor(1343)   (Show Source): (Show Source):
You can put this solution on YOUR website! P = 2x + 2y, where y = the length of the rectangle
The area, A = x*y
From the first equation, y = P/2 - x
Thus A = (P/2 - x)x
The area will be maximized if dA/dx = 0
dA/dx = P/2 - 2x = 0
This gives x = P/4
Thus y = P/2 - P/4 = P/4
x = y = P/4, which implies the rectangle must be a square
|
|
|