Question 111874: Determine whether the graph of each parabola opens upward or downward.
y=-1/2x2+3
Are the ordered pairs x=-3 and 2 1/2 and y=3 and -10?
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Determine whether the graph of each parabola opens upward or downward.
We know that:
quadratic function is
 , ,
and its graph is a
If 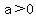 , it opens , it opens 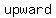
If 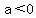 , it opens , it opens 
your parabola is:

As you can see  , that means , that means 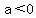 }; consequently, your parabola opens }; consequently, your parabola opens 
Are the ordered pairs x=-3 and 2 1/2 and y=3 and -10?
ordered pairs ( , ,  ) are : ( ) are : ( , ,  ) and ( ) and (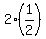 , ,  ) )
 evaluating our function for (
evaluating our function for ( , ,  ) )


 .. multiply both sides by
.. multiply both sides by 


 and for (
and for ( , ,  ) )


 multiply both sides by
multiply both sides by 


ordered pairs ( , ,  ) and ( ) and (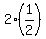 , ,  ) are not on the graph of the function ) are not on the graph of the function
| Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc) |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=6 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 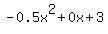 can be factored: can be factored:

Again, the answer is: -2.44948974278318, 2.44948974278318.
Here's your graph:
 |
|
|
|