Question 1118675: Suppose the annual cost per active-duty armed service member in a certain country increased from $80,000 in 1995 to $90,000 in 2000. In 1990, there were 2 million armed service personnel and this number decreased to 1.5 million in 2000. Use linear models for annual cost and personnel to estimate, to the nearest $10 million, the rate of change of total military personnel costs in 1998.
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! You may want linear models.
This is not a complete solution, but just a way to start analyzing the description. You want some data points.
Year Set to time 0=1990 Price Per Person/Service Member POINTS (t,p)
1995 5 80000 (5, 80000)
2000 10 90000 (10, 90000)
Year time 0=1990 Number of Service Members POINTS (t, n)
1990 0 2000000 (0,2000000)
2000 10 1500000 (10,1500000)
You use each pair of points to get linear equations for each. Next, COST would be price multiplied by number of members, or 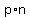 . Be careful to notice, the two first sets of data points are based on a different time point value; so you may need to compute the needed price to use for getting cost or Number of Members equation. . Be careful to notice, the two first sets of data points are based on a different time point value; so you may need to compute the needed price to use for getting cost or Number of Members equation.
The actual question is about year 1998, for when t=8.
|
|
|