Question 1117462: Demonstrate that the roots of the following equation are rational
abc²x² + 3a²cx + b²cx - 6a² - ab + 2b² = 0
Found 2 solutions by Edwin McCravy, greenestamps:
Answer by Edwin McCravy(20054)   (Show Source):
You can put this solution on YOUR website!
abc²x² + 3a²cx + b²cx - 6a² - ab + 2b² = 0
We put the left side
abc²x² + 3a²cx + b²cx - 6a² - ab + 2b²
in quadratic form: Ax² + Bx + C
(abc²)x² + (3a²cx + b²x) - 6a²-ab+2b²
(abc²)x² + (3a²c+b²)x + (-6a²-ab+2b²)
The x² term is abc²x² which has most likely
factorization (acx)•(bcx)
So I'll try to factor it like this:
[acx ][bcx ]
The constant term is
-6a² - ab + 2b²
That factors, take out a - sign
-(6a² + ab - 2b²)
and again as
-(2a - b)(3a + 2b)
So I'll try to factor the original left side as
one of these possible factorizations:
(1). [acx + (2a-b)][bcx - (3a+2b)]
(2). [acx - (2a-b)][bcx + (3a+2b)]
(3). [acx + (3a+2b)][bcx - (2a-b)]
(4). [acx - (3a+2b)][bck + (2a-b)]
I could multiply those out, but it would be easier to choose
arbitrary easy values for the letters and check their
results with the results of the original left side. Just
choose one of the letters as 0 and the rest as 1, so hopefully
only one of the four possible factorizations will be the same
as when we substitute them in the original left side. If two
or more are the same as that value, we'll have to make up
different values for the letters.
a = 0, b = c = x = 1
Substituting in possible factorization (1).
[acx + (2a-b)][bcx - (3a+2b)]
[0•1•1 + (2•0-1)][1•1•1 - (3•0+2•1)] = [0-1][1-2] = [-1][-1] = 1
Substituting in possible factorization (2).
[acx - (2a-b)][bcx + (3a+2b)]
[0•1•1 - (2•0-1)][1•1•1 + (3•0+2•1)] = [0+1][1+2] = [1][3] = 3
Substituting in possible factorization (3).
[acx + (3a+2b)][bcx - (2a-b)]
[0•1•1 + (3•0+2•1)][1•1•1 - (2•0-1)] = [0+2][1+1] = [2][2] = 4
Substituting in possible factorization (4).
[acx - (3a+2b)][bcx + (2a-b)]
[0•1•1 - (3•0+2•1)][1•1•1 + (2•0-1)] = [0-2][1-1] = [-2][0] = 0
That's good. They are all different. Now we can tell which one
is probably the correct factorization by substituting those same
values in the original left side:
a = 0, b = c = x = 1
abc²x² + 3a²cx + b²cx - 6a² - ab + 2b²
0•1•1²•1² + 3•0²•1•1 + 1²•1•x - 6•0² - 0•1 + 2•1²
0 + 0 + 1 - 0 - 0 + 2 = 3
So only possible factorization (2) can be the correct one.
But we really haven't shown that it is the correct one, but
only if any are correct, it's possible factorization (2).
So let's be sure:
(2). [acx - (2a-b)][bcx + (3a+2b)]
So pick arbitrary values for the letters, say
a=3, b=4, c=2, x=1
Substituting in (2)
(2). [acx - (2a-b)][bcx + (3a+2b)]
[3•2•1 - (2•3-4)][4•2•1 + (3•3+2•4)]
[6 - (6-4)][8 + (9+8)]
[6 - 2][8 + 17]
[4][25]
100
Substituting in the original left side:
a=3, b=4, c=2, x=1
3•4•2²•1² + 3•3²•2•1 + 4²•2•1 - 6•3² - 3•4 + 2•4²
3•4•4•1 + 3•9•2•1 + 16•2•1 - 6•9 - 3•4 + 2•16
48 + 54 + 32 - 54 - 12 + 32
100
Since we got the same 100, we are 99.999% sure that (2) is
the correct factorization. We can simplify (2) slightly as
(2). [acx - (2a-b)][bcx + (3a+2b)]
[acx - 2a + b][bcx + 3a + 2b]
So the original equation:
abc²x² + 3a²cx + b²cx - 6a² - ab + 2b² = 0
becomes
[acx - 2a + b][bcx + 3a + 2b] = 0
Using the zero factor property:
acx - 2a + b = 0; bcx + 3a + 2b = 0
acx = 2a - b
x =  <-- one root
bcx + 3a + 2b = 0
bcx = -3a - 2b
x = 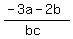 <-- other root
If a,b and c are rational and not 0, then both roots are
rational also.
Edwin
Answer by greenestamps(13200)  (Show Source):
|
|
|
