SOLUTION: A box with no top is to be constructed from a piece of cardboard whose length measures 10 inches more than its width. The box is formed by cutting squares that measure 3 inch on ea

The volume of the box is 225 cubic inches, while the height is 3 inches.

Hence, the base area is 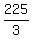  = 75 square inches.


Now, the original length of the cardboard was 10 inches more than its width.

When you folded the sides up,  the difference in dimensions of the base of the box remained the same:  10 inches.


Thus your base has the area of 75 square inches, and the difference between its length and its width is 10 inches.


What are two positive numbers, whose product is 75 and whose difference is 10 ?

But of course,  15 and 5.


So, your base has the dimensions 15 by 5 inches.



The get the original dimensions of the cardboard, you need to add 2 times 3 inches to each dimension of the base:

    15 + 2*3 = 21  and  5 + 2*3 = 11.

Thus the the original dimensions of the cardboard are 21 and 11 inches.


It is your answer.