SOLUTION: Find the first five terms in sequences with the following nth terms a.2n^2+2 b. 6n+2 c. 10n-3 d. 2n-1

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: Find the first five terms in sequences with the following nth terms a.2n^2+2 b. 6n+2 c. 10n-3 d. 2n-1       Log On


   

Question 1116129: Find the first five terms in sequences with the following nth terms
a.2n^2+2
b. 6n+2
c. 10n-3
d. 2n-1
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
What the question is asking is what is the value of each expression for n=1 , n=2 , n=3 , n=4 , and n=5 .
Plug in values for n , and find the result of each formula given.
It is not rocket science.

a. For the sequence whose terms are given by 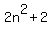2n%5E2%2B2 ,
For n=1 , the (first) term is 2%2A1%5E2%2B2=2%2A1%2B2=2%2B2=4 .
For n=2 , the (second) term is 2%2A2%5E2%2B2=2%2A4%2B2=8%2B2=10 .
For n=3 , the (third) term is 2%2A3%5E2%2B2=2%2A9%2B2=18%2B2=20 .
For n=4 , the (fourth) term is 2%2A4%5E2%2B2=2%2A16%2B2=32%2B2=34 .
For n=5 , the (fifth) term is 2%2A5%5E2%2B2=2%2A25%2B2=50%2B2=62 .
So, the first five terms are 4, 10, 20, 34, 62.
The expression 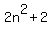2n%5E2%2B2 is a quadratic polynomial,
meaning a polynomial of degree 2.
As a function of n that expression is a quadratic function.

You can do the same for b, c, and d.
The expressions for b, c, and d are linear functions of n .

NOTE: The question was not difficult, so it must be leading to some conclusion.
If you calculate the differences between consecutive terms,
you will find that they are all the same for the terms given by
each of the linear expressions in b, c, and d.
If you calculate the differences between consecutive terms for the five terms
4, 10, 20, 34, and 62, given by the quadratic expression 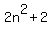2n%5E2%2B2 ,
you find that the "first differences" are 6, 10, 14, and 18:
10-4=6 , 20-10=10 , 34-20=14 , and 62-34=18 .
If you calculate the differences of the differences (the "second differences"),
you find:
10-6=4 , 14-10=4 , 18-14=4 .
For linear sequences, the first differences are the same.
For quadratic sequences, the second differences are the same.
That is probably where your teacher is going with this question.